Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T03:54:14.112Z Has data issue: false hasContentIssue false
  • English
  • Français

On Free Semigroups and Ramsey Numbers

Published online by Cambridge University Press:  20 November 2018

Gerard Lallement
Gerard Lallement*
Affiliation:
Pennsylvania State University, Pennsylvania16802
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If the length of a word w in a free semigroup F(X) satisfies 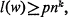, then for every partition of F(X) into k classes, w has n consecutive factors of length ≥p in the same class. As a consequence, the diagonal Ramsey numbers R(pn+1, p+1, k) have 1+pnk as lower bound.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 2 , 01 June 1974 , pp. 229 - 232
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Chvatal, V., Hypergraphs and Ramseyian theorems, Proc. Amer. Math. Soc. 27, (1971), 434-440.Google Scholar
2. Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. II, 1967, Amer. Math. Soc, Providence, R.I. Google Scholar
3. Erdös, P., Some remarks on the theory of graphs, Bull. Amer. Math. Soc. 53, 1947, 292-294.Google Scholar
4. Frasnay, C., Quelques problèmes combinatoires concernant les ordres totaux et les relations monomorphes, Ann. Inst. Fourier, Grenoble, 15, 1965, 415-524.Google Scholar
5. Ginsburg, S., The mathematical theory of context-free languages, 1966, McGraw-Hill.Google Scholar
6. Giraud, G. R., Une généralisation des nomblres et de Vinégalité de Schur, C.R. Acad. Se. Paris, t. 266 (1968), 437-440.Google Scholar
7. Greenwood, R. E. and Gleason, A. M., Combinatorial relations and chromatic graphs, Can. Journ. Math., 7, 1955, 1-7.Google Scholar
8. Hell, P., Ramsey Numbers, M.Sc. thesis, McMaster University, 1969.Google Scholar
9. Justin, J., Généralisation du théorème de Van der Waerden sur les semi-groupes répétitifs, J. Combinatorial Theory (A) 12, (1972), 357-367.Google Scholar
10. Ryser, H. J., Combinatorial mathematics, 1963, Cams Math. Monographs number 14.Google Scholar
11. Schützenberger, M. P., Quelques problèmes combinatoires de la théorie des automates, Cours de l’Institut de Programmation 1966–1967 rédigé par J. F. Perrot.Google Scholar