Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T20:01:06.887Z Has data issue: false hasContentIssue false
  • English
  • Français

On Finite-to-One Maps

Published online by Cambridge University Press:  20 November 2018

H. Murat Tuncali  and
Vesko Valov
H. Murat Tuncali
Affiliation:
Department of Mathematics, Nipissing University, 100 College Drive, P.O. Box 5002, North Bay, ON, P1B 8L7 e-mail: [email protected] e-mail: [email protected]
Vesko Valov
Affiliation:
Department of Mathematics, Nipissing University, 100 College Drive, P.O. Box 5002, North Bay, ON, P1B 8L7 e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 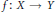$f:X\to Y$ be a 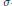$\sigma$-perfect 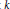$k$-dimensional surjective map of metrizable spaces such that dim 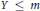$Y\le m$. It is shown that for every positive integer 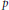$p$ with 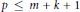$p\le m+k+1$ there exists a dense 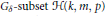${{G}_{\delta }}-\text{subset}\,\mathcal{H}\left( k,m,p \right)$ of 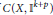$C\left( X,{{\mathbb{I}}^{k+p}} \right)$ with the source limitation topology such that each fiber of 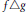$f\Delta g$, 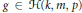$g\in \mathcal{H}\left( k,m,p \right)$, contains at most 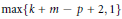$\max \left\{ k+m-p+2,1 \right\}$ points. This result provides a proof the following conjectures of S. Bogatyi, V. Fedorchuk and J. van Mill. Let 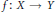$f:X\to Y$ be a 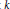$k$-dimensional map between compact metric spaces with dim 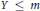$Y\le m$. Then: (1) there exists a map 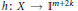$h:X\to {{\mathbb{I}}^{m+2k}}$ such that 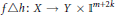$f\Delta h:\,X\to Y\times {{\mathbb{I}}^{m+2k}}$ is 2-to-one provided 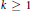$k\ge 1$; (2) there exists a map 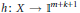$h:X\to {{\mathbb{I}}^{m+k+1}}$ such that 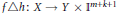$f\Delta h:X\to Y\times {{\mathbb{I}}^{m+k+1}}$ is 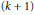$\left( k+1 \right)$-to-one.

Keywords

54F4555M1054C65Finite-to-one mapsdimensionset-valued maps
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 4 , 01 December 2005 , pp. 614 - 621
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Bogatyi, S., Fedorchuk, V. and van Mill, J., On mappings of compact spaces into Cartesian spaces. Topology Appl. 107(2000), no. 1-2, 13–24.Google Scholar
[2] Engelking, R., Theory of dimensions Finite and Infinite. Sigma Series in Pure Mathematics 10, Heldermann Verlag, Lemgo, 1995.Google Scholar
[3] Gutev, V. and Valov, V., Dense families of selections and finite-dimensional spaces. Set-Valued Anal. 11(2003), no. 4, 373–391.Google Scholar
[4] Krikorian, N., A note concerning the fine topology on function spaces. Compositio. Math. 21(1969), 343–348.Google Scholar
[5] Levin, M. and Lewis, W., Some mapping theorems for extensional dimension. Israel J. Math. 133(2003), 61–76.Google Scholar
[6] Michael, E., Continuous selections. I, Ann. of Math. 63(1956), 361–382.Google Scholar
[7] Munkres, J., Topology. Prentice Hall, Englewood Cliffs, NY, 1975.Google Scholar
[8] Pasynkov, B., On geometry of continuous maps of finite-dimensional metrizable compacta. Tr. Mat. Inst. Steklova 212(1996), no. 1, 147–172 (in Russian).Google Scholar
[9] Tuncali, H. M. and Valov, V., On dimensionally restricted maps Fund. Math. 175(2002), no. 1, 35–52.Google Scholar
[10] Tuncali, H. M. and Valov, V., On finite-dimensional maps Tsukuba J. Math. 28(2004), no. 1, 155–167.Google Scholar