Published online by Cambridge University Press: 20 November 2018
For any
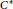 ${{C}^{*}}$
-algebra
${{C}^{*}}$
-algebra
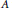 $A$
with an approximate unit of projections, there is a smallest ideal
$A$
with an approximate unit of projections, there is a smallest ideal
 $I$
of
$I$
of
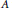 $A$
such that the quotient
$A$
such that the quotient
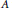 $A$
/
$A$
/
 $I$
is stably finite. In this paper a sufficient and necessary condition for an ideal of a
$I$
is stably finite. In this paper a sufficient and necessary condition for an ideal of a
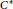 ${{C}^{*}}$
-algebra with real rank zero to be this smallest ideal is obtained by using
${{C}^{*}}$
-algebra with real rank zero to be this smallest ideal is obtained by using
 $K$
-theory
$K$
-theory