Hostname: page-component-cc8bf7c57-qfg88 Total loading time: 0 Render date: 2024-12-11T23:02:42.322Z Has data issue: false hasContentIssue false
  • English
  • Français

On Equal Products of Consecutive Integers

Published online by Cambridge University Press:  20 November 2018

R. A. Macleod  and
I. Barrodale
R. A. Macleod
Affiliation:
University of Victoria, Victoria, British Columbia
I. Barrodale
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using the theory of algebraic numbers, Mordell [1] has shown that the Diophantine equation

1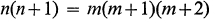

possesses only two solutions in positive integers; these are given by n = 2, m = 1, and n = 14, m = 5. We are interested in positive integer solutions to the generalized equation

2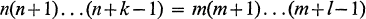

and in this paper we prove for several choices of k and l that (2) has no solutions, in other cases the only solutions are given, and numerical evidence for all values of k and l for which max (k, l) ≤ 15 is also exhibited.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 13 , Issue 2 , June 1970 , pp. 255 - 259
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Mordell, L. J., On the integer solutions of y(y+1) = x(x+1)(x+2), Pacific J. Math. 13B (1963), 1347-1351.Google Scholar