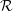Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balodi, Mamta
Banerjee, Abhishek
and
Ray, Samarpita
2020.
Cohomology of Modules Over -categories and Co--categories.
Canadian Journal of Mathematics,
Vol. 72,
Issue. 5,
p.
1352.
Balodi, Mamta
and
Banerjee, Abhishek
2023.
Fredholm modules over categories, Connes periodicity and classes in cyclic cohomology.
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G3,
p.
617.
Ahuja, Divya
and
Kour, Surjeet
2025.
Differential torsion theories on Eilenberg-Moore categories of monads.
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 3,
p.
107910.