Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T15:32:22.246Z Has data issue: false hasContentIssue false
  • English
  • Français

On Density of Generalized Polynomials

Published online by Cambridge University Press:  20 November 2018

N. Dyn ,
D. S. Lubinsky  and
Boris Shekhtman
N. Dyn
Affiliation:
Department of Mathematics, Tel-Aviv University, Ramat Aviv, Tel Aviv 61392, Israel
D. S. Lubinsky
Affiliation:
Department of Mathematics, Witwatersrand University, P.O. Wits 2050, Republic of South Africa
Boris Shekhtman
Affiliation:
Institute for Constructive Mathematics, Department of Mathematics, University of South Florida, Tampa, FL 33620, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the density in C[a, b] of generalized polynomials of the form 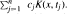The main point of this note is that total positivity of K(x, t) has little relationship to density: There is a symmetric, analytic, totally positive (in fact ETP (∞)) kernel K for which these generalized polynomials are not dense.

Keywords

Generalized polynomialsdensityclosuretotally positive kernelspositive kernels.41A3041A35.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 34 , Issue 2 , 01 June 1991 , pp. 202 - 207
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Achiezer, N. I., Theory of Approximation, (transi, by C. J. Hyman), Ungar, New York, 1956.Google Scholar
2. Dyn, N. and Lubinsky, D. S., Convergence of Interpolation to Transforms of Totally Positive Kernels, Can. J. Math., 40 (1988), 750–768.Google Scholar
3. Gierz, G. and Shekhtman, B., A Duality Principle for Rational Approximation, Pacific J. Math., 125 (1986), 79–92.Google Scholar
4. Gierz, G. and Shekhtman, B., On Spaces with Large Chebyshev Subspaces, J. Approx. Th., 54 (1988), 155— 161.Google Scholar
5. Karlin, S., The Existence of Eigenvalues for Integral Operators, Trans. Amer. Math. Soc, 113 (1964), 1–17.Google Scholar
6. Karlin, S., Total positivity and convexity preserving transformations, Proc. Sympos. Pure Math., 7 (1963), 329–347.Google Scholar