No CrossRef data available.
Article contents
On Complex Explicit Formulae Connected with the Möbius Function of an Elliptic Curve
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We study analytic properties function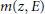 
$m\left( z,\,E \right)$, which is defined on the upper half-plane as an integral from the shifted 
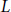$L$-function of an elliptic curve. We show that 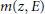$m\left( z,\,E \right)$ analytically continues to a meromorphic function on the whole complex plane and satisfies certain functional equation. Moreover, we give explicit formula for 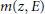$m\left( z,\,E \right)$ in the strip 
$\left| \Im z \right|\,<\,2\pi$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014
References
[1]
Bartz, K., On some complex explicit formulae connected with the Möbius function, I. Acta Arith. 57
(1991, 283–293.Google Scholar
[2]
Bateman, H. and Erdelyi, A., Higher transcendental functions. Vol. II, McGraw-Hill Book Company, 1953.Google Scholar
[3]
Breuil, C., Conrad, B., Diamond, F., and Taylor, R., On the modularity of elliptic curves over Q.
J. Amer. Math. Soc.
14
(2001, 843–939.http://dx.doi.org/10.1090/S0894-0347-01-00370-8
CrossRefGoogle Scholar
[4]
Iwaniec, H. and Kowalski, E., Analytic number theory.
Amer. Math. Soc., Providence, RI, 2003.Google Scholar
[5]
Kaczorowski, J., Results on the Möbius function.
J. London Math. Soc.
75
(2007, 509–521.http://dx.doi.org/10.1112/jlms/jdm006
CrossRefGoogle Scholar
[6]
Kaminski, D. and Paris, R. B., Asymptotics and Mellin–Barnes integrals. Encyclopedia Math. Appl., Cambridge University Press, Cambridge, 2001.Google Scholar
[7]
Perelli, A., General L-functions.
Ann. Mat. Pura Appl.
130
(1982, 287–306.http://dx.doi.org/10.1007/BF01761499
CrossRefGoogle Scholar
You have
Access