Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T11:05:03.314Z Has data issue: false hasContentIssue false
  • English
  • Français

On Characterizing the Multivariate Linear Exponential Distribution1

Published online by Cambridge University Press:  20 November 2018

D. G. Kabe
D. G. Kabe*
Affiliation:
St. Mary's University, Halifax 572
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If x and y are independent p component column vectors, and the conditional distribution of x, given x+y = z, is known, what can be said about the distributions of x and y? This problem has been solved by Seshadri (1966) in the particular case when the conditional distribution of x, given x+y = z, is multivariate normal. In fact Seshadri′s paper implicitly contains a characterization of the multivariate linear exponential distribution

(1)

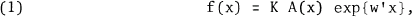
where A(x) is a function of x not involving the p component column vector w of constant terms.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 5 , October 1969 , pp. 567 - 572
Copyright
Copyright © Canadian Mathematical Society 1969

Footnotes

1

This research work was done while the author held a summer (1967) research fellowship of the Canadian Mathematical Congress.

References

1. Aczel, J., Lectures on functional equations and their applications. (Academic Press, New York, 1965).Google Scholar
2. Mathai, A.M., On the structural properties of the conditional distributions. Canad. Math. Bull. 10 (1967) 239–245.Google Scholar
3. Seshadri, V., A characteristic property of the multi-variate normal distribution. Ann. Math. Statist. 37 (1966) 1829–1831.Google Scholar