Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T18:23:55.984Z Has data issue: false hasContentIssue false
  • English
  • Français

On Certain Problems in the Theory of Sequences

Published online by Cambridge University Press:  20 November 2018

Rada Higgins
Rada Higgins*
Affiliation:
Department of Mathematics, The Ohio State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are well-acquainted with the theorem about sequences which states that, the existence of

(1)

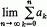
is sufficient to imply limk→∞ak = 0. Partially out of a growing interest in the theory of regularly varying sequences ([1]), and probably as an interesting problem, in and of itself, some mathematicians have tried to find conditions weaker than (1) that would guarantee limk→∞ak = 0.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 2 , June 1975 , pp. 229 - 231
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Bojanic, R. and Seneta, E., A unified theory of regularly varying sequences, Mathematische Zeitschrift, to appear.Google Scholar
2. Galambos, J. and Seneta, E., Regularly Varying Sequences (Technical Report 29, Series 2), Princeton University, 1973.Google Scholar
3. Higgins, R., A note on a problem in the theory of sequences, Elemente der Mathematik, to appear.Google Scholar
4. Niven, I. and Zuckerman, H. S., On certain sequences, American Math. Monthly 76 (1969), 386-389.Google Scholar