Hostname: page-component-5f745c7db-tvc9f Total loading time: 0 Render date: 2025-01-06T05:48:14.987Z Has data issue: true hasContentIssue false
  • English
  • Français

On Certain K-Groups Associated with Minimal Flows

Published online by Cambridge University Press:  20 November 2018

Jingbo Xia
Jingbo Xia*
Affiliation:
Department of Mathematics State University of New York at Buffalo Buffalo, New York 14214 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that the Toeplitz algebra associated with any flow which is both minimal and uniquely ergodic always has a trivial 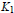${{K}_{1}}$-group. We show in this note that if the unique ergodicity is dropped, then such 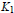${{K}_{1}}$-group can be non-trivial. Therefore, in the general setting of minimal flows, even the 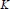$K$-theoretical index is not sufficient for the classification of Toeplitz operators which are invertible modulo the commutator ideal.

Keywords

46L8047B3547C15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 2 , 01 June 1998 , pp. 240 - 244
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Arveson, W., On groups of automorphisms of operator algebras. J. Funct.Anal. 15 (1974), 217–243.Google Scholar
2. Curto, R., Muhly, P. and Xia, J., Toeplitz operators on flows. J. Funct. Anal. 93 (1990), 391–450.Google Scholar
3. Douglas, R., Another look at real-valued index theory. (eds., J. B. Conway and B. B. Morel), Pitman Research Notes Math. Ser. 192, Longman Sci. Tech, 1988, 91–120.Google Scholar
4. Forelli, F., Analytic and quasi-invariant measures, Acta Math. 118 (1967), 33–59.Google Scholar
5. Muhly, P. and Putnam, I. and Xia, J., On the K-theory of some C*-algebras of Toeplitz and singular integral operators. J. Funct.Anal. 110 (1992), 161–225.Google Scholar
6. Muhly, P. and Xia, J., Commutator ideals and semicommutator ideals of Toeplitz algebras associated with flows. Proc. Amer. Math. Soc. 116 (1992), 1059–1066.Google Scholar
7. Muhly, P. and Xia, J., C*-algebras of singular integral operators and Toeplitz operators associated with n-dimensional flows. Internat. J. Math. 3 (1992), 525–579.Google Scholar
8. Pederson, G., C*-algebras and their automorphism groups. Academic Press, New York, 1979.Google Scholar
9. Tanaka, J.-I., Flows in fibers. Trans. Amer.Math. Soc. 343 (1994), 779–804.Google Scholar