Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T06:00:00.912Z Has data issue: false hasContentIssue false
  • English
  • Français

On Axiomatizability of Non-Commutative Lp-Spaces

Published online by Cambridge University Press:  20 November 2018

C. Ward Henson ,
Yves Raynaud  and
Andrew Rizzo
C. Ward Henson
Affiliation:
Mathematics Deptartment, University of Illinois at Urbana-Champaign, 1409 W. Green Street, Urbana, IL 61801, U.S.A.
Yves Raynaud
Affiliation:
Institut de Mathématiques de Jussieu (CNRS), Projet Analyse Fonctionnelle, Case 186, 4 place Jussieu, 75252 Paris, Cedex 05 France
Andrew Rizzo
Affiliation:
Cross and Blue Shield of Illinois, 300 East Randolph Street, Chicago, IL 60601, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that Schatten 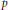$p$-classes of operators between Hilbert spaces of different (infinite) dimensions have ultrapowers which are (completely) isometric to non-commutative 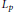${{L}_{p}}$-spaces. On the other hand, these Schatten classes are not themselves isomorphic to non-commutative 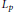${{L}_{p}}$ spaces. As a consequence, the class of non-commutative 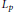${{L}_{p}}$-spaces is not axiomatizable in the first-order language developed by Henson and Iovino for normed space structures, neither in the signature of Banach spaces, nor in that of operator spaces. Other examples of the same phenomenon are presented that belong to the class of corners of non-commutative 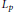${{L}_{p}}$-spaces. For 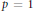$p\,=\,1$ this last class, which is the same as the class of preduals of ternary rings of operators, is itself axiomatizable in the signature of operator spaces.

Keywords

46L5203C6546B2046L0746M07
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 519 - 534
Copyright
Copyright © Canadian Mathematical Society 2007

References

[AL] Arazy, J. and Lindenstrauss, J., Some linear topological properties of the space Cp of operators on Hilbert space. Compositio Math. 30(1975), 81–111.Google Scholar
[DCK] Dacunha-Castelle, D. and Krivine, J.-L., Application des ultraproduits à l’étude des espaces et algèbres de Banach. Studia Math. 41(1972), 315–334.Google Scholar
[Di] Dixmier, J., Von Neumann Algebras. Second edition. North-Holland mathematical Library 27, North Holland, Amsterdam, 1981.Google Scholar
[EOR] Effros, E., Ozawa, N., and Ruan, Z.-J., On injectivity and nuclearity for operator spaces. Duke Math. J. 110(2001), no. 3, 489–521.Google Scholar
[G] Groh, U., Uniform ergodic theorems for identity preserving Schwartz maps on W*-algebras. J. Operator Theory 11(1984), no. 2, 395–404.Google Scholar
[H] Haagerup, U., Lp-spaces associated with an arbitrary von Neumann algebra. In: Algèbres d’Opérateurs et leurs applications en physique mathématique, Colloques internationaux du CNRS 274, 1979, CNRS, Paris, pp. 175–184.Google Scholar
[Ha] Harris, L. A., Bounded symmetric homogeneous domains in infinite dimensional spaces. In: Proceedings on Infinite Dimensional Holomorphy. Lectures Notes in Math. 364, Springer-Verlag, Berlin, 1974.Google Scholar
[He] Henson, C. W., Nonstandard hulls of Banach spaces. Israel J. Math 25(1976), no. 1–2, 108–144.Google Scholar
[HI] Henson, C. W. and Iovino, J., Ultraproducts in analysis. In: Analysis and Logic. London Math. Soc. Lecture Note Ser. 262, Cambridge University Press, Cambridge, 2003.Google Scholar
[LT] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. II. Function Spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete 97, Springer-Verlag, Berlin, 1979.Google Scholar
[L] Lacey, H. E., The Isometric Theory of Classical Banach Spaces. Die Grundlehren der MathematischenWissenschaften 208, Springer-Verlag, New York, 1974.Google Scholar
[M] Marcolino Nhany, J. L., La stabilité des espaces Lp non-commutatifs. Math. Scand. 81(1997), no. 2, 212–218.Google Scholar
[MC] McCarthy, C. A., Cp . Israel J. Math. 5(1967), 249–271.Google Scholar
[NO] Ng, P. W. and Ozawa, N., A characterization of completely 1-complemented subspaces of noncommutative L 1 -spaces. Pacific J. Math. 205(2002), no. 1, 171–195.Google Scholar
[Pi] Pisier, G., Introduction to Operator Space Theory. London Mathematical Society Lecture Note Series 294, Cambridge University Press, Cambridge, 2003.Google Scholar
[R] Raynaud, Y., On ultrapowers of non-commutative Lp spaces. J. Operator Theory 48(2002), no. 1, 41–68.Google Scholar
[RX] Raynaud, Y. and Xu, Q., On subspaces of non-commutative Lp-spaces. J. Funct. Anal. 203(2003), no. 1, 149–196.Google Scholar
[Ru] Ruan, Z.-J., Type decomposition and rectangular AFD property for W*-TRO’s. Canad. J. Math. 56(2004), no. 4, 843–870.Google Scholar
[S] Sherman, D., Non-commutative Lp-structure encodes exactly Jordan structure. J. Funct. Anal. 221(2005), no. 1, 150–166.Google Scholar
[T] Terp, M., Lp-spaces Associated with von Neumann Algebras. Notes, Copenhagen University, 1981.Google Scholar
[Y] Youngson, M. A., Completely contractive projections on C*-algebras. Quart. J. Math. Oxford 34(1983), no. 136, 507–511.Google Scholar
[Z] Zettl, H., A characterization of ternary rings of operators. Adv. in Math. 48(1983), no. 2, 117–143.Google Scholar