Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T03:44:10.020Z Has data issue: false hasContentIssue false
  • English
  • Français

On Arithmetic Means of Sequences Generated by a Periodic Function

Published online by Cambridge University Press:  20 November 2018

Giovanni Fiorito
Giovanni Fiorito*
Affiliation:
Dipartimento di Matematica Università di Catania viale Andrea Doria 6 Catania I-95125 Italy, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove the convergence of arithmetic means of sequences generated by a periodic function 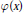$\varphi (X)$, moreover if 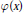$\varphi (X)$ satisfies a suitable symmetry condition, we prove that their limit is 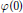$\varphi (0)$. Applications of previous results are given to study other means of sequences and the behaviour of a class of recursive series.

Keywords

40A05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 184 - 189
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Bary, N. K., A Treatise on Trigonometric Series Vol. II. Pergamon Press, 1964.Google Scholar
[2] Edwards, R. E., Fourier Series A Modern Introduction Vol. I. Holt, Rinehart and Winston, Inc., 1967.Google Scholar
[3] Fiorito, G., Musmeci, R. and Strano, M., Diophantine approximations and convergence of series in Banach spaces. Matematiche (Catania) XLVIII(1993), Fasc. II, 349–358.Google Scholar
[4] Fiorito, G., Uniforme distribuzione ed applicazioni ad una classe di serie ricorrenti. Matematiche (Catania) XLVIII(1993), Fasc. I, 123–133.Google Scholar
[5] Hardy, G. and Wright, E., An introduction to the theory of numbers. Clarendon Press, Oxford, 1954.Google Scholar
[6] Knopp, K., Theory and application of infinite series. Hafner Publishing Company, New York, 1971.Google Scholar
[7] Kuipers, L. and Niederreiter, H., Uniform distribution of sequences. J. Wiley & Sons, New York, 1974.Google Scholar