Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-10T18:09:59.218Z Has data issue: false hasContentIssue false
  • English
  • Français

On Approximation by Fejér Means to Periodic Functions Satisfying a Lipschitz Condition

Published online by Cambridge University Press:  20 November 2018

Lee Lorch
Lee Lorch*
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

S. M. Nikolski [4, Theorem 1; cf. 3, esp. pp. 144 and 148] considered the remainder term in the approximation by the n-th Fejér mean, σn(x), to a function, f(x), of period 2π satisfying a Lipschitz condition of order α, 0<α≤1. In this connection, he introduced the quantity

1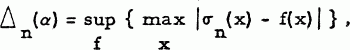

where the maximum is taken over all x and the supremum is taken over all functions of period 2π, bounded by 1 (a notational convenience only) and satisfying a Laps chitz condition of order α.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 5 , Issue 1 , January 1962 , pp. 21 - 27
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Lee, Lorch, Asymptotic Expressions for some Integrals which include certain Lebesgue and Féjer Constants, Duke Math. Journal, vol. 20(1953), pp. 89-104.Google Scholar
2. Lee, Lorch, The Principal Term in the Asymptotic Expansion of the Lebesgue Constants, Amer. Math. Monthly, vol. 61(1954), pp. 245-249.Google Scholar
3. LP. Natanson, Konstruktive Funktionentheorie, (German translation from Russian), Berlin, 1955.Google Scholar
4. Nikolski, S. M., Sur I'allure asymptotique du reste dans I'approximation au moyen des sommes de Fejér des fonctions vérifiant la condition de Lipschitz (Russian, French summary), Izvestiya Akad. Nauk SSSR. Seria Mat. (Bull, de TAcad. des Sciences de I'uRSS. Série Math.) vol. 4 (1940), pp. 501-508.Google Scholar
5. Sz.-Nagy, B., Approximation der Funktionen durch die arithmetischen Mittel ihrer Fourierschen Reihen, Acta Scientiarum Ma thematic a rum (Szeged), vol. 11 (1946-48), pp. 71-84.Google Scholar