Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-18T21:04:18.991Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Upper Bound for the Heat Kernel on SU*(2n)/ Sp(n)

Published online by Cambridge University Press:  20 November 2018

P. Sawyer
P. Sawyer*
Affiliation:
Department of Mathematics, University of Ottawa, Ottawa, Ontario, K1N 6N5
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Jean-Philippe Anker made an interesting conjecture in [2] about the growth of the heat kernel on symmetric spaces of noncompact type. For any symmetric space of noncompact type, we can write

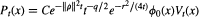
where ϕ0 is the Legendre function and q, "the dimension at infinity", is chosen such that limt—>∞Vt(x) = 1 for all x. Anker's conjecture can be stated as follows: there exists a constant C > 0 such that

where is the set of positive indivisible roots. The behaviour of the function ϕ0 is well known (see [1]).

The main goal of this paper is to establish the conjecture for the spaces SU*(2n)/ Sp(n).

Keywords

Primary: 58G30secondary: 53C3558G11
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 3 , 01 September 1994 , pp. 408 - 418
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Anker, Jean-Philippe, La forme exacte de Vestimation fondamentale de Harish-Chandra, C. R. Acad. Sci. Paris Sér. 1305(1987), 371–374.Google Scholar
2. Anker, Jean-Philippe, Le noyau de la chaleur sur les espaces symétriques U(p, q)/U(p) x U(q), Lecture Notes in Math. 1359, Springer-Verlag, New York, 1988, 60–82.Google Scholar
3. Beerends, R. J., The Abel transform and shift operators, Comp. Math. 66(1988), 145–197.Google Scholar
4. Beerends, R. J., A transmutation property of the generalized Abel transform associated with root system A2, Indag. Math. (N.S.) (2) 1(1990), 155–168.Google Scholar
5. Chalykh, O. A. and Veselov, A. P., Commutative rings of partial differential operators and Lie algebras, Comm. Math. Phys. 126(1990), 597–611.Google Scholar
6. Davies, E. B., Heat kernels and spectral theory, Cambridge Univ. Press, 1989.Google Scholar
7. Gangolli, R., Asymptotic behaviour of spectra of compact quotients of certain symmetric spaces, Acta Math. 121(1968), 151–192.Google Scholar
8. Helgason, Sigurdur, Group and Geometric Analysis, Academic Press, New York, 1984.Google Scholar
9. Koornwinder, T. H., Jacobi transformations and analysis on noncompact semisimple Lie groups. In: Spectral functions: group theoretical aspects and applications, (eds. Laskey, R. A., et. al), Reidel, 1984.Google Scholar
10. Opdam, E. M., Root systems and hype rgeome trie functions III, Comp. Math. 67(1988), 21–49.Google Scholar
11. Riesz, Marcel, L'intégrale de Riemann-Liouville et le problème de Cauchy, Acta Math. 81(1949), 1–223.Google Scholar
12. Sawyer, Patrice, The heat equation on the symmetric space associated to SL(n, R), thesis, McGill University, 1989.Google Scholar
13. Sawyer, Patrice, The heat equation on the spaces of positive definite matrices, Canad. J. Math. (3) 44(1992), 624– 651.Google Scholar
14. Veselov, A. P. and Chalykh, O. A., Explicit formulas for spherical functions on symmetric spaces of type A II,Functional Anal. Appl. (1) 26(1992), 59–60.Google Scholar