Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-03T20:03:06.307Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Elementary Problem in Number Theory

Published online by Cambridge University Press:  20 November 2018

Paul Erdös
Paul Erdös*
Affiliation:
University of Toronto
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A question which Chalk and L. Moser asked me several years ago led me to the following problem: Let 0 < x ≤ y. Estimate the smallest f(x) so that there should exist integers u and v satisfying

1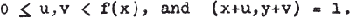

I am going to prove that for every ∊ > 0 there exist arbitrarily large values of x satisfying

2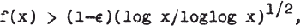

but that for a certain c > 0 and all x

3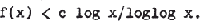

A sharp estimation of f(x) seems to be a difficult problem. It is clear that f(p) = 2 for all primes p. I can prove that f(x)→ ∞ and f(x)/loglog x → 0 if we neglect a sequence of integers of density 0, but I will not give the proof here.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 1 , Issue 1 , 01 January 1958 , pp. 5 - 8
Copyright
Copyright © Canadian Mathematical Society 1958

References

* L. Moser informs me that he independently obtained this result and its generalization to an m-dimensional lattice.