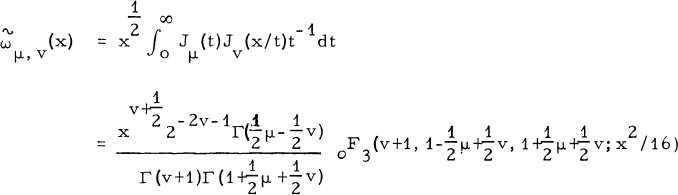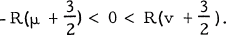Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dahiya, R.S
1976.
Operational calculus and self-reciprocal functions.
Indagationes Mathematicae (Proceedings),
Vol. 79,
Issue. 1,
p.
17.
Dixit, Atul
Kesarwani, Aashita
and
Kumar, Rahul
2022.
Explicit transformations of certain Lambert series.
Research in the Mathematical Sciences,
Vol. 9,
Issue. 2,


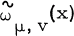 was defined by G.N. Watson, [9, (i)]in 1931 by the integral relation
was defined by G.N. Watson, [9, (i)]in 1931 by the integral relation