Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T10:01:05.058Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Sum of Divisors

Published online by Cambridge University Press:  20 November 2018

Hisashi Yokota
Hisashi Yokota*
Affiliation:
Department of Mathematics Hiroshima Institute of Technology Itsukaichi, Hiroshima Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let l(N, r) be the minimum number of terms needed to express r as a sum of distinct divisors of N. Let l(N) = max{l(N, r) : 1 ≤ r ≤ N}. Then for Vose's sequence 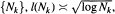improving the result of M. Vose.

Keywords

11D8511D68
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 423 - 430
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Erdős, P., The solution in whole numbers of the equation:1 /x1 + 1/x2 + • • • + 1/xn = a/b, Mat. Lapok 1(1950), 192–210.Google Scholar
2. Erdős, P. and Graham, R. L., Old and New Problems and Results in Combinatorial Number Theory , Monographie 28, L'Enseign. Math. Univ. de Genève (1980), 30–44.Google Scholar
3. Tenenbaum, G., Sur un problème extremal en arithmétique, Ann. Inst. Fourier (22) 37 (1987), 1–18.Google Scholar
4. Tenenbaum, G. and Yokota, H., Length and denominators of Egyptian fractions, III , J. Number Theory 35(1990), 150–156.Google Scholar
5. Vose, M., Integers with consecutive divisors in small ratio, J. Number Theory 19(1984), 233–238.Google Scholar