Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T17:55:42.292Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Riemannian Manifold M 2n with an Almost Tangent Structure

Published online by Cambridge University Press:  20 November 2018

C.S. Houh
C.S. Houh*
Affiliation:
Wayne State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Professor Eliopoulous studied almost tangent structures on manifolds M2n in [1; 2]. An almost tangent structure F is a field of class C∞ of linear operations on M2n such that at each point x in M2n, Fx maps the complexified tangent space 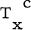into itself and that Fx is of rank n everywhere and satisfies that F2 = 0. In this note, we consider a (1,1) tensor field 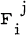. on a Riemannian M2n which satisfies 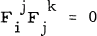everywhere and is such that the rank of F is n everywhere. Such 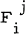gives an almost tangent structure F on M2n.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 6 , December 1969 , pp. 759 - 769
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Eliopoulos, H.A., Structures presque tangents sur les variétés differentiables. C. R. Acad. Se. Paris. 255 (1962) 1563–1565.Google Scholar
2. Eliopoulos, H.A., On the general theory of differentiable manifolds with almost tangent structure. Canad. Math. Bull. 8 (1965) 721–748.Google Scholar
3. Hsu, C.J., On some structures which are similar to the quaternion structure. Tôhoku Math. J. 12 (1960) 403–428.Google Scholar
4. Yano, K., Affine connexions in an almost product space. Kodai Math. Sem. Reports 11 (1959) 1–24.Google Scholar
5. Yano, K., On a structure defined by a tensor field f of type (1,1) satisfying f3 + f = 0, Tensor, N.S. 14 (1963) 99–109.Google Scholar