On a rationality problem for fields of cross-ratios II

Abstract

Let k be a field, $x_1, \dots , x_n$ be independent variables and let 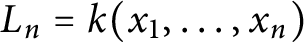$L_n = k(x_1, \dots , x_n)$ . The symmetric group 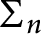$\operatorname {\Sigma }_n$ acts on 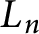$L_n$ by permuting the variables, and the projective linear group 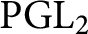$\operatorname {PGL}_2$ acts by

$$ \begin{align*} \begin{pmatrix} a & b \\ c & d \end{pmatrix}\, \colon x_i \longmapsto \frac{a x_i + b}{c x_i + d} \end{align*} $$

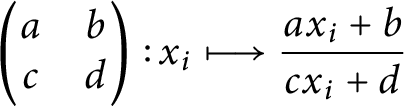
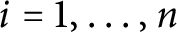for each $i = 1, \dots , n$ . The fixed field 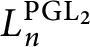$L_n^{\operatorname {PGL}_2}$ is called “the field of cross-ratios”. Given a subgroup 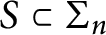$S \subset \operatorname {\Sigma }_n$ , H. Tsunogai asked whether 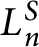$L_n^S$ rational over 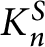$K_n^S$ . When 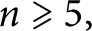$n \geqslant 5,$ the second author has shown that 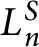$L_n^S$ is rational over 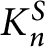$K_n^S$ if and only if S has an orbit of odd order in $\{ 1, \dots , n \}$ . In this paper, we answer Tsunogai’s question for 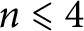$n \leqslant 4$ .