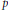Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Friedlander, John B.
Hansen, Jan
and
Shparlinski, Igor E.
2000.
Character sums with exponential functions.
Mathematika,
Vol. 47,
Issue. 1-2,
p.
75.
Shparlinski, Igor E.
2002.
Security of most significant bits of gx2.
Information Processing Letters,
Vol. 83,
Issue. 2,
p.
109.
Lin, Bochui
and
Qi, Wenfeng
2006.
Generators by the quadratic exponential method.
Journal of Electronics (China),
Vol. 23,
Issue. 6,
p.
915.