Article contents
On a Few Diophantine Equations Related to Fermat’s Last Theorem
Published online by Cambridge University Press: 20 November 2018
Abstract
We combine the deep methods of Frey, Ribet, Serre and Wiles with some results of Darmon, Merel and Poonen to solve certain explicit diophantine equations. In particular, we prove that the area of a primitive Pythagorean triangle is never a perfect power, and that each of the equations 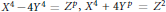 ${{X}^{4}}\,-\,4{{Y}^{4}}\,=\,{{Z}^{p}},\,{{X}^{4}}\,+\,4{{Y}^{p}}\,=\,{{Z}^{2}}$ has no non-trivial solution. Proofs are short and rest heavily on results whose proofs required Wiles’ deep machinery.
${{X}^{4}}\,-\,4{{Y}^{4}}\,=\,{{Z}^{p}},\,{{X}^{4}}\,+\,4{{Y}^{p}}\,=\,{{Z}^{2}}$ has no non-trivial solution. Proofs are short and rest heavily on results whose proofs required Wiles’ deep machinery.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2002
References
- 1
- Cited by


