Article contents
On a conjecture of M. R. Murty and V. K. Murty
Published online by Cambridge University Press: 25 October 2022
Abstract
Let
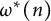 $\omega ^*(n)$
be the number of primes p such that
$\omega ^*(n)$
be the number of primes p such that
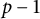 $p-1$
divides n. Recently, M. R. Murty and V. K. Murty proved that
$p-1$
divides n. Recently, M. R. Murty and V. K. Murty proved that
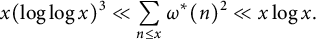 $$ \begin{align*}x(\log\log x)^3\ll\sum_{n\le x}\omega^*(n)^2\ll x\log x.\end{align*} $$
$$ \begin{align*}x(\log\log x)^3\ll\sum_{n\le x}\omega^*(n)^2\ll x\log x.\end{align*} $$
They further conjectured that there is some positive constant C such that
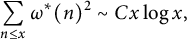 $$ \begin{align*}\sum_{n\le x}\omega^*(n)^2\sim Cx\log x,\end{align*} $$
$$ \begin{align*}\sum_{n\le x}\omega^*(n)^2\sim Cx\log x,\end{align*} $$
as
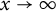 $x\rightarrow \infty $
. In this short note, we give the correct order of the sum by showing that
$x\rightarrow \infty $
. In this short note, we give the correct order of the sum by showing that
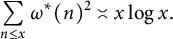 $$ \begin{align*}\sum_{n\le x}\omega^*(n)^2\asymp x\log x.\end{align*} $$
$$ \begin{align*}\sum_{n\le x}\omega^*(n)^2\asymp x\log x.\end{align*} $$
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The author is supported by the National Natural Science Foundation of China under Grant No. 12201544, the Natural Science Foundation of Jiangsu Province of China under Grant No. BK20210784, and the China Postdoctoral Science Foundation under Grant No. 2022M710121. He is also supported by the foundation numbers JSSCBS20211023 and YZLYJF2020PHD051.
References
- 1
- Cited by



