Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T11:42:54.611Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Conjecture of Livingston

Published online by Cambridge University Press:  20 November 2018

Siddhi Pathak
Siddhi Pathak*
Affiliation:
Department of Mathematics and Statistics, Queen’s University, Kingston, ON K6L 3N6 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

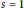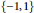In an attempt to resolve a folklore conjecture of Erdös regarding the non-vanishing at $s\,=\,1$ of the $L$-series attached to a periodic arithmetical function with period $q$ and values in $\left\{ -1,\,1 \right\}$, Livingston conjectured the 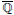$\overline{\mathbb{Q}}$-linear independence of logarithms of certain algebraic numbers. In this paper, we disprove Livingston’s conjecture for composite 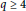$q\,\ge \,4$, highlighting that a new approach is required to settle Erdös conjecture. We also prove that the conjecture is true for prime 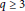$q\,\ge \,3$, and indicate that more ingredients will be needed to settle Erdös conjecture for prime $q$.

Keywords

11J8611J72non-vanishing of L-serieslinear independence of logarithms of algebraic numbers
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 184 - 195
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Baker, A., Transcendental number theory. Cambridge University Press, London-New York, 1975.Google Scholar
[2] Baker, A., Birch, B. J., and Wirsing, E. A., On a problem ofChowla. J. Number Theory 5(1973), 224–236. http://dx.doi.Org/10.1 01 6/0022-314X(73)90048-6 Google Scholar
[3] Davis, H. T., The summation of series. Principia Press of Trinity University, San Antonia, Tex., 1962.Google Scholar
[4] Hurwitz, A., Einige Eigenschaften der Dirichlet Funktionen F(s) = Y.(D/n)n s> diebei der Bestimmung der Klassenzahlen Binârer quadratischer Formen auftreten. Zeitschrift f. Math. u. Physik 27(1882), 86–101.+diebei+der+Bestimmung+der+Klassenzahlen+Binârer+quadratischer+Formen+auftreten.+Zeitschrift+f.+Math.+u.+Physik+27(1882),+86–101.>Google Scholar
[5] Livingston, A. E., The series Y.7=\ f (n) / n for periodic f. Canad. Math. Bull. 8(1965), no. 4, 413–432. http://dx.doi.Org/10.4153/CMB-1965-029-2 Google Scholar
[6] Ram Murty, M., Problems in analytic number theory. Graduate Texts in Mathematics, 206, Readings in Mathematics, Springer, New York, 2008.Google Scholar
[7] Ram Murty, M. and Sardha, N., Euler-Lehmer constants and a conjecture ofErdb's. J. Number Theory 130(2010), no. 12, 2671–2682. http://dx.doi.Org/10.101 6/j.jnt.2O10.07.004 Google Scholar
[8] Ram Murty, M. and Sinha, K., The generalized Dedekind determinant. In: SCHOLAR—a scientific celebration highlighting open lines of arithmetic research, Contemp. Math., 655, American Mathematical Society, Providence, RI, 2015, pp. 153–164. http://dx.doi.Org/!0.1090/conm/655/13232 Google Scholar