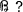Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Toft, B
1974.
Color-critical graphs and hypergraphs.
Journal of Combinatorial Theory, Series B,
Vol. 16,
Issue. 2,
p.
145.
Abbott, H. L.
1975.
On Property of Families of Sets.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 1,
p.
133.
de Vries, Hans Ludwig
1977.
On property B and on Steiner systems.
Mathematische Zeitschrift,
Vol. 153,
Issue. 2,
p.
155.
Abbott, H. L.
and
Liu, A. C.
1978.
The existence problem for colour critical linear hypergraphs.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 32,
Issue. 3-4,
p.
273.
Abbott, H.L
Liu, A
and
Toft, B
1980.
The enumeration problem for color critical linear hypergraphs.
Journal of Combinatorial Theory, Series B,
Vol. 29,
Issue. 1,
p.
106.
Abbott, H. L.
and
Hare, D. R.
1989.
Sparse color-critical hypergraphs.
Combinatorica,
Vol. 9,
Issue. 3,
p.
233.
1994.
Graph Coloring Problems.
p.
261.
Abbott, H. L.
Zhou, B.
and
Hare, D. R.
1994.
Sparse color‐critical graphs and hypergraphs with no short cycles.
Journal of Graph Theory,
Vol. 18,
Issue. 4,
p.
373.
1994.
Graph Coloring Problems.
p.
231.
Abbott, H.L.
Hare, D.R.
and
Zhou, B.
1998.
Color-critical graphs and hypergraphs with few edges and no short cycles.
Discrete Mathematics,
Vol. 182,
Issue. 1-3,
p.
3.
Kostochka, Alexandr
Mubayi, Dhruv
Rödl, Vojtěch
and
Tetali, Prasad
2001.
On the chromatic number of set systems.
Random Structures & Algorithms,
Vol. 19,
Issue. 2,
p.
87.
Райгородский, Андрей Михайлович
Raigorodskii, Andrei Mikhailovich
Райгородский, Андрей Михайлович
Raigorodskii, Andrei Mikhailovich
Шабанов, Дмитрий Александрович
Shabanov, Dmitrii Aleksandrovich
Шабанов, Дмитрий Александрович
and
Shabanov, Dmitrii Aleksandrovich
2011.
Задача Эрдеша - Хайнала о раскрасках гиперграфов, ее обобщения и смежные проблемы.
Успехи математических наук,
Vol. 66,
Issue. 5,
p.
109.
Östergård, Patric R.J.
2014.
On the minimum size of 4-uniform hypergraphs without propertyB.
Discrete Applied Mathematics,
Vol. 163,
Issue. ,
p.
199.
Mathews, Jithin
Panda, Manas Kumar
and
Shannigrahi, Saswata
2015.
On the construction of non-2-colorable uniform hypergraphs.
Discrete Applied Mathematics,
Vol. 180,
Issue. ,
p.
181.
Lebedeva, A. V.
2016.
On Algorithmic Methods of Analysis of Two-Colorings of Hypergraphs.
Journal of Mathematical Sciences,
Vol. 213,
Issue. 2,
p.
211.
Raigorodskii, Andrei Mikhailovich
and
Cherkashin, Danila Dmitrievich
2020.
Экстремальные задачи в раскрасках гиперграфов.
Успехи математических наук,
Vol. 75,
Issue. 1(451),
p.
95.
Raigorodskii, A. M.
and
Cherkashin, D. D.
2020.
Extremal problems in hypergraph colourings.
Russian Mathematical Surveys,
Vol. 75,
Issue. 1,
p.
89.
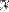 of sets is said to possess property
of sets is said to possess property 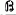 if there exists a set
if there exists a set 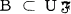 such that
such that 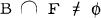 and
and 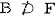 for every
for every 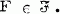 We consider the following question raised by P. Erdös |1|: let n and N be positive integers, n ≥ 2 and N ≥ 2n - 1 and let S be a set of N elements; what is the least integer
We consider the following question raised by P. Erdös |1|: let n and N be positive integers, n ≥ 2 and N ≥ 2n - 1 and let S be a set of N elements; what is the least integer 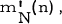 (provided such an integer exists), for which there exists a family
(provided such an integer exists), for which there exists a family 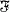 of
of 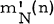 subsets of S satisfying
subsets of S satisfying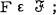
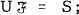
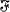 does not have property
does not have property 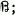
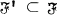 and
and 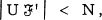 then
then 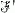 has property
has property