Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1994.
Korovkin-type Approximation Theory and its Applications.
p.
555.
Lecué, Guillaume
2007.
Simultaneous adaptation to the margin and to complexity in classification.
The Annals of Statistics,
Vol. 35,
Issue. 4,
Dikmen, Akif Barbaros
and
Lukashov, Alexey
2016.
Generating functions method for classical positive operators, their q-analogues and generalizations.
Positivity,
Vol. 20,
Issue. 2,
p.
385.


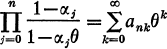
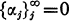 is a sequence of complex numbers. if 0 < α
is a sequence of complex numbers. if 0 < α