Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Israel, Jay E
1968.
Convergence of metric nuclei.
Journal of Approximation Theory,
Vol. 1,
Issue. 4,
p.
444.
Israel, Jay E
1968.
Entropic determination of a metric nucleus.
Journal of Approximation Theory,
Vol. 1,
Issue. 2,
p.
189.


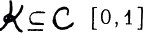 containing those functions for which
containing those functions for which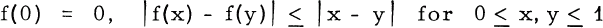
 ; it is just a compact blur in the infinite-dimensional space
; it is just a compact blur in the infinite-dimensional space  . Nevertheless, we want to establish that it shares with several other sets an odd but rather remarkable "geometric" property: it is overwhelmingly concentrated around a single element. This element we call the nucleus of
. Nevertheless, we want to establish that it shares with several other sets an odd but rather remarkable "geometric" property: it is overwhelmingly concentrated around a single element. This element we call the nucleus of 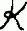 .
.