Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-08T16:35:30.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Notes on Numerical Analysis IV. On Accelerating Iteration Procedures With Superlinear Convergence

Published online by Cambridge University Press:  20 November 2018

Wesley Kotzé
Wesley Kotzé*
Affiliation:
McGill University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the study of algorithms for the iterative solution of an arbitrary analytic equation f(z) = 0, acceleration procedures are of importance in practice and of considerable interest in the theory of the subject. Let

.

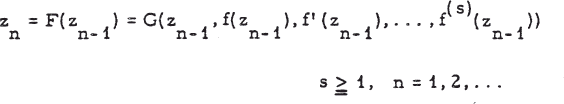be an iteration formula which has a zero ξ of f(z) as attractive fixed point. An algorithm of this type is said to converge towards a root ξ of f(z) = 0 for all initial approximations z = z0 in a vicinity of ξ, of order k > 0, when

1.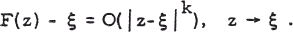

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 7 , Issue 3 , September 1964 , pp. 425 - 430
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. Kotzé, W., On infinitely many algorithms for the solution of an analytic equation, Thesis for the degree M.Sc. (McGill University, 1961). An abstract of this thesis appeared in Canad. Math. Bull, vol.5, no. 1 (1962), pp.108-109.Google Scholar
2. Frame, J. S., A variation of Newton's method,Amer. Math. Monthly 51, (1944), pp. 36–38.Google Scholar
3. Schrőder, E., Űber unendlich viele Algorithmen zur Auflősung der Gleichungen, Math. Ann. 2, (1870), pp. 317–365.Google Scholar
4. Schwerdtfeger, H., Notes on Numerical Analysis I. Polynomial Iteration, Canad. Math. Bull., vol.2, no. 2 (1959), pp.97–109.Google Scholar