No CrossRef data available.
Article contents
A Note on Upper Bounds for the Eigenvalues of y″ + λpy=0
Published online by Cambridge University Press: 20 November 2018
Extract
The natural modes of a small planar transversal vibration of a fixed string of unit length and tension are determined by the eigenvalues and associated eigenfunctions of the differential equation
(1)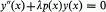
subject to the boundary condition
(2)
where the non-negative function p describes the mass distribution of the string. That the distribution of mass on the string influences the modes of vibration, may be reflected by observing that the eigenvalues determined by the system (1–2) may be considered functions of the density p, λn(p), where λ1(p)<λ2(p)<….
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1975


