A Note on the Tarry-Escott Problem

Extract

The Tarry-Escott problem in Diophantine analysis is the following: consider the system of equations

1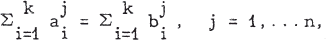

for the unknowns a₁, …, a_k, b₁, …, b_k, what is the smallest integer K = K(n) in the set of all k! s for which the system (1) possesses a non - trivial solution in integers ? By an integer we mean a rational integer and a solution is called trivial if the sets { a₁, …, a_k} and {b₁, …, b_k} are permutations of each other. By the Tarry-Escott problem one may also mean the problem of finding an actual solution of (1) or finding all such solutions but we shall be concerned with the bound K(n) only. However, the method given here is constructive, that is to say, with each estimate K for K it leads to finding actual non - trivial solutions of (1) with k = K₁.