Article contents
A note on the phase retrieval of holomorphic functions
Published online by Cambridge University Press: 08 October 2020
Abstract
We prove that if f and g are holomorphic functions on an open connected domain, with the same moduli on two intersecting segments, then
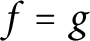 $f=g$
up to the multiplication of a unimodular constant, provided the segments make an angle that is an irrational multiple of
$f=g$
up to the multiplication of a unimodular constant, provided the segments make an angle that is an irrational multiple of
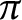 $\pi $
. We also prove that if f and g are functions in the Nevanlinna class, and if
$\pi $
. We also prove that if f and g are functions in the Nevanlinna class, and if
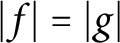 $|f|=|g|$
on the unit circle and on a circle inside the unit disc, then
$|f|=|g|$
on the unit circle and on a circle inside the unit disc, then
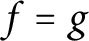 $f=g$
up to the multiplication of a unimodular constant.
$f=g$
up to the multiplication of a unimodular constant.
Keywords
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The author was supported by the CHED-PhilFrance scholarship from Campus France and the Commission of Higher Education (CHED), Philippines.
References
- 3
- Cited by



