Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T08:36:51.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the Kasparov Product of C*-algebra Extensions

Published online by Cambridge University Press:  20 November 2018

Changguo Wei
Changguo Wei*
Affiliation:
School of Mathematical Sciences, Ocean University of China, Qingdao, 266100, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using the Dadarlat isomorphism, we give a characterization for the Kasparov product of 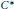${{C}^{*}}$-algebra extensions. A certain relation between 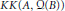$KK\left( A,\,Q\left( B \right) \right)$ and 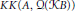$KK\left( A,\,Q\left( KB \right) \right)$ is also considered when $B$ is not stable, and it is proved that 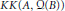$KK\left( A,\,Q\left( B \right) \right)$ and 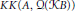$KK\left( A,\,Q\left( KB \right) \right)$ are not isomorphic in general.

Keywords

46L80extensionKasparov productKK-group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 4 , 01 December 2013 , pp. 870 - 880
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Blackadar, B., K-theory for operator algebras. Second ed. Mathematical Sciences Research Institute Publications, 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[2] Brown, L. G., Douglas, R. G., and Fillmore, P. A., Extensions of C*-algebras and K-homology. Ann. of Math. (2) 105 (1977), no. 2, 265–324. http://dx.doi.org/10.2307/1970999 Google Scholar
[3] Cuntz, J., Generalized homomorphisms between C*-algebras and KK-theory. In: Dynamics and processes (Bielefeld, 1981), Lecture Notes in Mathematics, 1031, Springer, Berlin, 1983, pp. 31–45. [4] M. Dadarlat, Approximate unitary equivalence and the topology of Ext(A; B). In: C*-algebras (M¨unster, 1999) Springer, Berlin, 2000, pp. 42–60.Google Scholar
[5] Elliott, G. A., Gong, G., and Li, L., On the classification of simple inductive limit C*-algebras. II. The isomorphism theorem. Invent. Math. 168 (2007), no. 2, 249–320. http://dx.doi.org/10.1007/s00222-006-0033-y Google Scholar
[6] Higson, N., A characterization of KK-theory. Pacific J. Math. 126 (1987), no. 2, 253–276.Google Scholar
[7] Jensen, K. and Thomsen, K., Elements of KK-theory. Mathematics: Theory & Applications, Birkhäuser Boston, Boston, MA, 1991.Google Scholar
[8] Kasparov, G. G., The operator K-functor and extensions of C*-algebras. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 44 (1980), no. 3, 571–636, 719.Google Scholar
[9] Lin, H., An introduction to the classification of amenable C*-algebras. World Scientific Publishing Co., Inc., River Edge, NJ, 2001.Google Scholar
[10] Lin, H., Classification of simple C*-algebras and higher dimensional noncommutative tori. Ann. of Math. (2) 157 (2003), no. 2, 521–544. http://dx.doi.org/10.4007/annals.2003.157.521 Google Scholar
[11] Lin, H., Classification of simple C*-algebras of tracial topological rank zero. Duke Math. J. 125 (2004) no. 1, 91–119. http://dx.doi.org/10.1215/S0012-7094-04-12514-X Google Scholar
[12] Lin, H., Full extensions and approximate unitary equivalences. Pacific J. Math. 229 (2007), no. 2, 389–428. http://dx.doi.org/10.2140/pjm.2007.229.389 Google Scholar
[13] Lin, H., Extensions by simple C*-algebras: quasidiagonal extensions. Canad. J. Math. 57 (2005), no. 2, 351–399. http://dx.doi.org/10.4153/CJM-2005-016-5 Google Scholar
[14] Lin, H., Asymptotic unitary equivalence and classification of simple amenable C*-algebras. Invent. Math. 183 (2010), no. 2, 385–450. http://dx.doi.org/10.1007/s00222-010-0280-9 Google Scholar
[15] MacLane, S., Homology. Die Grundlehren der mathematischenWissenschaften, 114, Springer-Verlag, Berlin-New York, 1967.Google Scholar
[16] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
[17] Rørdam, M., Classification of extensions of certain C*-algebras by their six term exact sequences in K-theory. Math. Ann. 308 (1997), no. 1, 93–117. http://dx.doi.org/10.1007/s002080050067 Google Scholar
[18] Rørdam, M. and E. Størmer, Classification of nuclear C*-algebras. Entropy in Operator Algebras. Encyclopaedia of Mathematical Sciences, 126,Operator Algebras and Non-commutative Geometry, 7, Springer-Verlag, Berlin, 2002.Google Scholar
[19] Rosenberg, J. and Schochet, C., The K¨unneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. 55 (1987), no. 2, 431–474. http://dx.doi.org/10.1215/S0012-7094-87-05524-4 Google Scholar
[20] Wei, C., Universal coefficient theorems for the stable Ext-groups. J. Funct. Anal. 258 (2010), no. 2, 650–664. http://dx.doi.org/10.1016/j.jfa.2009.10.009 Google Scholar
[21] Wei, C., Classification of extensions of AT-algebras. International J. Math. 22 (2011), no. 8, 1187–1208. http://dx.doi.org/10.1142/S0129167X11007227 Google Scholar