Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kozyrev, V. P.
1974.
Graph theory.
Journal of Soviet Mathematics,
Vol. 2,
Issue. 5,
p.
489.
Zhou, Bo
and
Trinajstić, Nenad
2008.
Maximum eigenvalues of the reciprocal distance matrix and the reverse Wiener matrix.
International Journal of Quantum Chemistry,
Vol. 108,
Issue. 5,
p.
858.
Aouchiche, Mustapha
and
Hansen, Pierre
2013.
A survey of Nordhaus–Gaddum type relations.
Discrete Applied Mathematics,
Vol. 161,
Issue. 4-5,
p.
466.
Dankelmann, P.
Guo, Y.
Rivett-Carnac, E.J.
and
Volkmann, L.
2025.
The oriented diameter of graphs derived from other graphs.
Discrete Mathematics,
Vol. 348,
Issue. 6,
p.
114443.


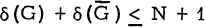
 is the complement of G.
is the complement of G.