Hostname: page-component-f554764f5-sl7kg Total loading time: 0 Render date: 2025-04-11T07:27:42.891Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Normal Matrices

Published online by Cambridge University Press:  20 November 2018

Marvin Marcus  and
Nisar Khan
Marvin Marcus
Affiliation:
U. S. National Bureau of Standards, Washington, D. C. and Muslim University, Aligarh, India and University of British Columbia
Nisar Khan
Affiliation:
U. S. National Bureau of Standards, Washington, D. C. and Muslim University, Aligarh, India and University of British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1954 A.J. Hoffman and O. Taussky [1] showed that if A is an n-square complex matrix with eigenvalues λ = (λ1, …, λn ) and P is a permutation matrix for which αA + βA* has eigenvalues 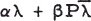for some αβ ≠ 0 then A is normal. Here 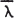is the conjugate vector of λ. As a companion result they also proved that if the eigenvalues of AA* are , i = 1, …, n then A is normal.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 4 , Issue 1 , January 1961 , pp. 23 - 27
Copyright
Copyright © Canadian Mathematical Society 1961

References

Hoffman, A.J. and Taussky, O., A characterization of normal matrices, J. Research, Nat. Bur. Standards 52 (1954), 17-19.Google Scholar