Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-30T16:51:06.254Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on Integers Representable by Binary Quadratic Forms

Published online by Cambridge University Press:  20 November 2018

Kenneth S. Williams
Kenneth S. Williams*
Affiliation:
Carleton University, Ottawa, Ontario, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B be the set of positive integers prime to d which are representable by some primitive, positive, integral binary quadratic form of discriminant d. It is the purpose of this note to show that the following asymptotic estimate for the number of integers in B less than or equal to x can be proved using only elementary arguments:

(1)

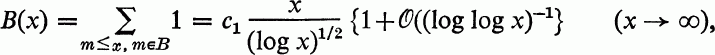
where c1 is the positive constant given in (17) below. (Using the deeper methods of complex analysis James [2] has proved this result with the error term 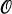((log x)-1/2) replacing 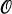((log log x)-1). Heupel [1] using a transcendental method as in James [2] improved this to 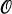((log x)-1).)

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 123 - 125
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Heupel, W., Die Verteilung der gangen Zahlen, die durch quadratische Formen dargestellt werden. Archiv. der. Math., 19 (1968), 162-166.Google Scholar
2. James, R. D., The distribution of integers represented by quadratic forms, Amer. J. Math., 60 (1938), 737-744.Google Scholar
3. Landau, E., Primzahlen, Chelsea Publishing Co., N.Y. (1953), second edition.Google Scholar
4. Pall, G., The distribution of integers represented by binary quadratic forms, Bull. Amer. Math. Soc, (1943), 447-449.Google Scholar
5. Rieger, G. J., Zahlentheoretische Anwendung eines Taubersatzes mit Restgied, Math. Ann., 182 (1969), 243-248.Google Scholar
6. Rieger, G. J., Zum Satz von Landau über die Summe aus zwei Quadraten, Jour, für die reine und angewandte Math., 244 (1970), 198-200.Google Scholar
7. Selberg, A., An elementary proof of the prime number theorem for arithmetic progressions, Canad. J. Math., 2 (1950), 66-78.Google Scholar
8. Uchiyama, S., On some products involving primes, Proc. Amer. Math. Soc, 28 (1971), 629–630.Google Scholar
9. Wirsing, E., Elementare Beweise des Primzahlsatzes mit Restglied II, Jour, für die reine und angewandte Math., 214/215 (1964), 1-18.Google Scholar