Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T01:09:40.117Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Geometric Factoriality

Published online by Cambridge University Press:  20 November 2018

S. M. Bhatwadekar  and
K. P. Russell
S. M. Bhatwadekar
Affiliation:
Tata Institute of Fundamental Research, Bombay, India
K. P. Russell
Affiliation:
Department of Mathematics and Statistics and CICMA, McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k: be a perfect field such that 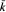is solvable over k. We show that a smooth, affine, factorial surface birationally dominated by affine 2-space 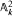is geometrically factorial and hence isomorphic to 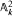. The result is useful in the study of subalgebras of polynomial algebras. The condition of solvability would be unnecessary if a question we pose on integral representations of finite groups has a positive answer.

Keywords

13F2014M0520C05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 38 , Issue 4 , 01 December 1995 , pp. 390 - 395
Copyright
Copyright © Canadian Mathematical Society 1995

References

[B-D] Bhatwadekar, S. M. and Dutta, A., On residual variables and stably polynomial algebras, Comm. Algebra, to appear.Google Scholar
[F] Fujita, T., On Zarishi problem, Proc. Japan Acad. (A) 55(1979), 106–110.Google Scholar
[L] Lang, S., Rapport sur le cohomologie des groupes, W. A. Benjamin, New York, Amsterdam, 1966.Google Scholar
[K] Kambayashi, T., On the absence of non-trivial separable forms of the affine plane, J. Algebra 35(1975), 449–456.Google Scholar
[M-S] Miyanishi, M. and Sugie, T., Affine surfaces containing cylinderlike open sets, J. Math. Kyoto Univ. 20(1980), 11–42.Google Scholar
[R-l] Russell, K. P., On affine-ruled rational surfaces, Math. Ann. 255(1981), 287–302.Google Scholar
[R-2] Russell, K. P., Simple birational extensions of two dimensional rational domains, Compositio Math. 33( 1976), 197–208.Google Scholar
[R-S] Russell, K. P. and Sathaye, A., On finding and cancelling variables in k[X, Y,Z], J. Algebra 57(1979), 153–166.Google Scholar