No CrossRef data available.
Article contents
Note on Generalized Schreier Extensions of Groups
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
By a (generalized) Schreier extension we mean a group G decomposed into a subinvariant series Gn ↣ Gn-1 ↣ Gn-2 … ↣ G1 ↣ G0 = Gn is anti-invariant in G, i. e. the only subgroup of G which is normal in Gn is the trivial one. ( “ ↣ ” denotes a group monomorphism, i. e. an injection homomorphism. ) As is well known, such groups G can be embedded into the repeated wreath product 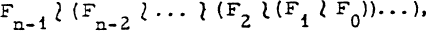 where Fi ≅ Gi / Gi+1 (cf. [ 2 ], notation of M. Hall [ 1 ], p. 81).
where Fi ≅ Gi / Gi+1 (cf. [ 2 ], notation of M. Hall [ 1 ], p. 81).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1966
References
2.
Krasner, M. - Kaloujnine, L., Produits complet de groupes de permutations et problème d' extension de groupes. Acta Szeged, 14, 1951, 69-82.Google Scholar
3.
Neumann, B.H., Hanna, Neumann and Neumann, Peter M., Wreath products and varieties of groups, Math. Z. 80, 44-62 (1962).Google Scholar


