Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-18T21:45:36.049Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Exact Colimits

Published online by Cambridge University Press:  20 November 2018

John R. Isbell
John R. Isbell*
Affiliation:
Case Western Reserve University, Cleveland, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note proves another special case of a conjecture of U. Oberst. Oberst considered [1], for any small category 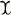, the X abelian category 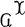of abelian group-valued functors on , and the X functor Colim: 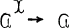which takes each diagram to its colimit. The question is, when is Colim exact? For its relationships, see [1], It is a sufficient condition that each component of is upward filtered. Oberst conjectured that it is also necessary, and proved this under some conditions. He mentioned particularly the case that 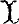is a monoid, i.e. a category with one object. We shall verify the conjecture in that case.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 4 , October 1968 , pp. 569 - 572
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Oberst, U., Homology of categories and exactness of direct limits, to appear.Google Scholar
2. Oberst, U. and Röhrl, H., Singular homology with sheaf coefficients, to appear.Google Scholar