Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-15T20:31:37.542Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on composition operators on the disc and bidisc

Part of: Spaces and algebras of analytic functions Holomorphic functions of several complex variables

Published online by Cambridge University Press:  24 March 2025

Athanasios Beslikas Open the ORCID record for Athanasios Beslikas [Opens in a new window]
Athanasios Beslikas*
Affiliation:
Doctoral School of Exact and Natural Studies, Institute of Mathematics, Faculty of Mathematics and Computer Science, Jagiellonian University, Łojasiewicza 6, Cracow PL30348, Poland
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we give a new necessary condition for the boundedness of the composition operator on the Dirichlet-type space on the disc, via a two dimensional change of variables formula. With the same formula, we characterize the bounded composition operators on the anisotropic Dirichlet-type spaces 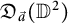$\mathfrak {D}_{\vec {a}}(\mathbb {D}^2)$ induced by holomorphic self maps of the bidisc 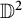$\mathbb {D}^2$ of the form 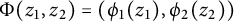$\Phi (z_1,z_2)=(\phi _1(z_1),\phi _2(z_2))$. We also consider the problem of boundedness of composition operators 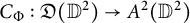$C_{\Phi }:\mathfrak {D}(\mathbb {D}^2)\to A^2(\mathbb {D}^2)$ for general self maps of the bidisc, applying some recent results about Carleson measures on the Dirichlet space of the bidisc.

Keywords

Dirichlet-type spacescomposition operators

MSC classification

Primary: 32A37: Other spaces of holomorphic functions (e.g. bounded mean oscillation (BMOA), vanishing mean oscillation (VMOA)) 30H20: Bergman spaces, Fock spaces
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 14
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author was partially supported by the National Science Center, Poland, SHENG III, research project 2023/48/Q/ST1/00048.

References

Aleman, A., Hilbert spaces of analytic functions between the Hardy and the Dirichlet space . Proc. Amer. Math. Soc. 115(1992), 97–104.Google Scholar
Arcozzi, N., Rochberg, R., Sawyer, E. T., and Wick, B. D., The Dirichlet space: A survey . New York J. Math. 17a(2011), 45–86.Google Scholar
Arcozzi, N., Mozolyako, P., Perfekt, K.-M., and Sarfatti, G., Bi-parameter potential theory and Carleson measures for the Dirichlet space on the bidisc . Discrete Anal. 22(2023), 57 pp.Google Scholar
Arcozzi, N., Chalmoukis, N., Levi, M., and Mozolyako, P., Two-weight dyadic Hardy inequalities . Rend. Lincei Mat. Appl. 34(2023), 657–714. https://doi.org/10.4171/RLM/1023 Google Scholar
Balooch, A. and Wu, Z., A new formalization of Dirichlet-type spaces . J. Math. Anal. Appl. 526(2023), no. 1, 127322.Google Scholar
Bayart, F., Composition operators on the Hardy Space of the tridisc. Preprint, arXiv:2312.02565v1.Google Scholar
Bayart, F., Composition operators on the polydisk induced by affine maps . J. Funct. Anal. 260(2011), no. 7, 1969–2003.Google Scholar
El-Fallah, O., Kellay, K., Mashreghi, J., and Ransford, T., A primer on the Dirichlet space, Cambridge Tracts in Mathematics, 203, Cambridge University Press, University Printing House, Cambridge CB2 SBS, United Kingdom, 2014.Google Scholar
El-Fallah, O., Kellay, K., Mashreghi, J., and Ransford, T. J., One-box conditions for Carleson measures for the Dirichlet space . Proc. Amer. Math. Soc. 143(2015), no. 2, 679–684.Google Scholar
Kaptanoglu, H. T., Mobius-invariant Hilbert spaces in polydiscs . Pacific J. Math. 163(1994), no. 2, pp. 337–360.Google Scholar
Knese, G., Kosinski, Ł., Ransford, T. J., and Sola, A., Cyclic polynomials in anisotropic Dirichlet spaces . JAMA 138(2019), 23–47. https://doi.org/10.1007/s11854-019-0014-x Google Scholar
Kosinski, Ł., Composition operators on the polydisc . J. Funct. Anal. 284(2023), no. 5, 109801.Google Scholar
Mozolyako, P., Psaromiligkos, G., Volberg, A., and Zorin-Kranich, P., Carleson embedding on tri-tree and on tri-disc. Preprint. https://doi.org/10.48550/arXiv.2001.02373 Google Scholar
Pau, J. and Perez, P. A., Composition operators acting on weighted Dirichlet spaces . J. Math. Anal. Appl. 401(2013), no. 2, 682–694.Google Scholar
Shapiro, J. H., The essential norm of a composition operator . Ann. Math. 12(1987), 375–404.Google Scholar
Stegenga, D., Multipliers of the Dirichlet space . Illinois J. Math. 24(1980), no. 1, 113–139, Spring.Google Scholar