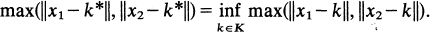Hostname: page-component-f554764f5-fnl2l Total loading time: 0 Render date: 2025-04-08T16:35:34.026Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Best Simultaneous Approximation in Normed Linear Spaces

Published online by Cambridge University Press:  20 November 2018

Arne Brøndsted
Arne Brøndsted*
Affiliation:
University of Copenhagen, Denmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of the present note is to point out that the results of D. S. Goel, A. S. B. Holland, C. Nasim and B. N. Sahney [1] on best simultaneous approximation are easy consequences of simple facts about convex functions. Given a normed linear space X, a convex subset K of X, and points x1, x2 in X, [1] discusses existence and uniqueness of K* ∈ K such that

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 19 , Issue 3 , 01 September 1976 , pp. 359 - 360
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Goel, D. S., Holland, A. S. B., Nasim, C. and Sahney, B. N., On best simultaneous approximation in normed linear spaces, Canad. Math. Bull. 17 (1974), pp. 523–527.Google Scholar