Article contents
A Note on Algebras that are Sums of Two Subalgebras
Published online by Cambridge University Press: 20 November 2018
Abstract
We study an associative algebra
 $A$
over an arbitrary field that is a sum of two subalgebras
$A$
over an arbitrary field that is a sum of two subalgebras
 $B$
and
$B$
and
 $C$
(i.e.,
$C$
(i.e.,
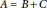 $A\,=\,B+C$
). We show that if
$A\,=\,B+C$
). We show that if
 $B$
is a right or left Artinian
$B$
is a right or left Artinian
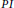 $PI$
algebra and
$PI$
algebra and
 $C$
is a
$C$
is a
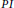 $PI$
algebra, then
$PI$
algebra, then
 $A$
is a
$A$
is a
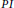 $PI$
algebra. Additionally, we generalize this result for semiprime algebras
$PI$
algebra. Additionally, we generalize this result for semiprime algebras
 $A$
. Consider the class of all semisimple finite dimensional algebras
$A$
. Consider the class of all semisimple finite dimensional algebras
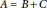 $A\,=\,B+C$
for some subalgebras
$A\,=\,B+C$
for some subalgebras
 $B$
and
$B$
and
 $C$
that satisfy given polynomial identities
$C$
that satisfy given polynomial identities
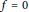 $f\,=\,0$
and
$f\,=\,0$
and
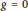 $g\,=\,0$
, respectively. We prove that all algebras in this class satisfy a common polynomial identity.
$g\,=\,0$
, respectively. We prove that all algebras in this class satisfy a common polynomial identity.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2016
References
- 6
- Cited by


