Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T20:19:33.372Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on 3-choosability of Planar Graphs Related to Montanssier’s Conjecture

Published online by Cambridge University Press:  20 November 2018

Haihui Zhang
Haihui Zhang*
Affiliation:
School of Mathematical Science, Huaiyin Normal University, 111 Changjiang West Road, Huaian, Jiangsu, 223300, P. R. China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a given list assignment 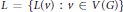$L\,=\,\{L\left( v \right)\,:\,v\,\in \,V\left( G \right)\}$, a graph 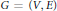$G\,=\,\left( V,\,E \right)$ is $L$-colorable if there exists a proper coloring $c$ of 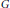$G$ such that 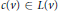$c\left( v \right)\,\in \,L\left( v \right)$ for all 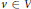$v\,\in \,V$. If 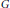$G$ is $L$-colorable for every list assignment $L$ having 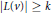$\left| L\left( v \right) \right|\,\ge \,k$ for all 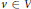$v\,\in \,V$, then 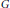$G$ is said to be $k$-choosable. Montassier (Inform. Process. Lett. 99 (2006) 68-71) conjectured that every planar graph without cycles of length 4, 5, 6, is 3-choosable. In this paper, we prove that every planar graph without 5-, 6- and 10-cycles, and without two triangles at distance less than 3 is 3-choosable.

Keywords

05C15choosabilityplanar graphcycle
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 440 - 448
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Alonand, N. Tarsi, M., Colorings and orientations of graphs.Combinatorica 12(1992), no. 2, 125–134. http://dx.doi.org/10.1007/BF01204715 Google Scholar
[2] Chen, M., Montassier, M., and Raspaud, A., Some structural properties of planar graphs and their applications to 3-choosability. Discrete Math. 312(2012), no. 2, 362–373. http://dx.doi.org/10.1016/j.disc.2011.09.028 Google Scholar
[3] Dvorak, Z., 3-choosabiliy of planar graphs with (<4)-cycles far apart. J. Combin. Theory Ser. B 104(2014) 28–59. http://dx.doi.org/10.1016/j.jctb.2013.10.004 Google Scholar
[4] Dvorak, Z., Lidicky, B., and Skrekovski, R., Planar graphs without 3-, 7-, and 8-cycles are 3-choosable. Discrete Math.309(2009), no. 20, 5899–5904.http://dx.doi.org/10.1016/j.disc.2009.04.010 Google Scholar
[5] Erdos, P., Rubin, A. L., and Taylor, H., Choosability in graphs. In: Proceedings of the West Coast Conference on Combinatorics, Graph Theory and Computing (Humboldt State Univ., Arcata, Calif., 1979), Congress.Numer., 26, Utilitas Math, Winnipeg, MB, 1980, pp. 125–157.Google Scholar
[6] Farzad, B., Planar graphs without 7 -cycles are 4-choosable. SIAM J. Discrete Math.23(2009), no. 3. 1179–1199. http://dx.doi.org/10.1137/05064477X Google Scholar
[7] Fijavz, G., Juvan, M., Mohar, B., and Skrekovski, R., Planar graphs without cycles of specific lengths. Europ. J. Combin. 23(2002), no. 4, 377–388. http://dx.doi.org/10.1006/eujc.2002.0570 Google Scholar
[8] Gutner, S., The complexity ofplanar graph choosability. Discrete Math. 159(1996), no. 1-3, 119–130. http://dx.doi.org/10.1016/0012-365X(95)00104-5 Google Scholar
[9] Lam, P. C. B., Xu, B., and Liu, J., The 4-choosability of plane graphs without 4-cycles. J. Combin. Theory Ser. B 76(1999), no. 1, 117–126. http://dx.doi.org/10.1006/jctb.1998.1893 Google Scholar
[10] Lam, P. C. B., Shiu, W., and Xu, B., On structure of some plane graphs with application to choosability. J. Combin. Theory Ser B, 82(2001), no. 2, 285–297. http://dx.doi.org/10.1006/jctb.2001.2038 Google Scholar
[11] Lam, P. C. B. Shiu, W., and Song, Z., The 3-choosability of plane graphs of girth 4. Discrete Math. 294(2005), no. 3, 297–301. http://dx.doi.org/10.1016/j.disc.2004.10.023 Google Scholar
[12] Lovasz, L., Combinatorial problems and exercises. North-Holland Publishing Co., Amsterdam-New York, 1979.Google Scholar
[13] Mirzakhani, M., A small non-4-choosableplanar graph. Bull. Inst. Combin. Appl. 17(1996), 15–18.Google Scholar
[14] Montassier, M., Raspaud, A., and Wang, W., Bordeaux 3-color conjecture and 3-choosability. Discrete Math. 306(2006), no. 6, 573–579. http://dx.doi.org/10.1016/j.disc.2006.02.001 Google Scholar
[15] Montassier, M., A note on the not 3-choosability of some families of planar graphs. Inform. Process. Lett. 99(2006), no. 2, 68–71. http://dx.doi.org/10.1016/j.ipl.2005.10.014 Google Scholar
[16] Thomassen, C., Every planar graph is 5-choosable. J. Combin. Theory Ser. B 62(1994), no. 1, 180–181. http://dx.doi.org/10.1006/jctb.1994.1062 Google Scholar
[17] Thomassen, C. ,3-list-coloringplanar graph of girth 5.J. Combin. Theory, Ser. B 64(1995), no. 1, 101–107. http://dx.doi.org/10.1006/jctb.1995.1027 Google Scholar
[18] Voigt, M., List colourings of planar graphs. Discrete Math. 120(1993), no. 1-3, 215–219. http://dx.doi.org/10.1016/0012-365X(93)90579-I Google Scholar
[19] Voigt, M., A not 3-choosable planar graph without 3-cycles. Discrete Math. 146( 1995), no. 1-3, 325–328. http://dx.doi.org/10.1016/0012-365X(94)00180-9 Google Scholar
[20] Wang, W.-F., Planar graphs that have no short cycles with a chord are 3-choosable. Taiwanese J. Math. 11(2007), no. 1, 179–186.Google Scholar
[21] Wang, W. and Lih, K.-W, Choosability and edge choosability of planar graphs without five cycles.Appl. Math.Lett. 15(2002), no. 5, 561–565. http://dx.doi.org/10.1016/S0893-9659(02)80007-6 Google Scholar
[22] Wang, W., Choosability and edge choosability of planar graph without intersecting triangles.SIAM J. Discrete Math. 15(2002), no. 4, 538–545. http://dx.doi.org/10.1137/S0895480100376253 Google Scholar
[23] Wang, Y., Lu, H., and Chen, M., A note on 3-choosability of planar graphs.Inform. Process.Lett. 105(2008), no. 5, 206–211. http://dx.doi.org/10.1016/j.ipl.2007.08.027 Google Scholar
[24] Xu, B., (4m, m)-choosability of plane graphs. J. Syst. Sci. Complex. 14(2001), no. 2, 174–178.Google Scholar
[25] Zhang, H., Xu, B., andZ. Sun, Every plane graph with girth at least 4 without 8-and 9-circuits is 3-choosable. ArsCombin. 80(2006), 247–257.Google Scholar