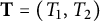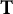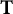1 Introduction
Let
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {K}$
be Hilbert spaces, and let
$\mathcal {K}$
be Hilbert spaces, and let
![]() $\mathcal {B}( \mathcal {H},\mathcal {K})$
be the algebra of bounded linear operators from
$\mathcal {B}( \mathcal {H},\mathcal {K})$
be the algebra of bounded linear operators from
![]() $ \mathcal {H}$
to
$ \mathcal {H}$
to
![]() $\mathcal {K}$
. If
$\mathcal {K}$
. If
![]() $\mathcal {H}=\mathcal {K}$
, we write
$\mathcal {H}=\mathcal {K}$
, we write
![]() $ \mathcal {B(H)}:=\mathcal {B}(\mathcal {H},\mathcal {H})$
. For an operator
$ \mathcal {B(H)}:=\mathcal {B}(\mathcal {H},\mathcal {H})$
. For an operator
![]() $ S\in \mathcal {B}(\mathcal {H},\mathcal {K})$
, the kernel of S is denoted by
$ S\in \mathcal {B}(\mathcal {H},\mathcal {K})$
, the kernel of S is denoted by
![]() $ \mathrm {ker}(S)$
and the range of S is denoted by
$ \mathrm {ker}(S)$
and the range of S is denoted by
![]() $\mathrm {ran}(S)$
. The linear pencil of an ordered pair
$\mathrm {ran}(S)$
. The linear pencil of an ordered pair
![]() $\mathbf {T}=(T_{1},T_{2})$
of operators
$\mathbf {T}=(T_{1},T_{2})$
of operators
![]() $T_{1}$
and
$T_{1}$
and
![]() $T_{2}$
in
$T_{2}$
in
![]() $\mathcal {B(H)}$
is defined by
$\mathcal {B(H)}$
is defined by
![]() $\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, and the linear pencil of
$\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, and the linear pencil of
![]() $\mathbf {T}=(T_{1},T_{2})$
at
$\mathbf {T}=(T_{1},T_{2})$
at
![]() $\lambda \in \mathbb {C}$
is defined by
$\lambda \in \mathbb {C}$
is defined by
![]() $\mathbb {T}_{\lambda }:=T_{1}-\lambda T_{2}$
. (For a detailed discussion of the linear pencil of
$\mathbb {T}_{\lambda }:=T_{1}-\lambda T_{2}$
. (For a detailed discussion of the linear pencil of
![]() $\mathbf {T}$
, the reader may refer to [Reference Bōgli and Marletta3, Reference Djordjević, Kim and Yoon7].) A subspace
$\mathbf {T}$
, the reader may refer to [Reference Bōgli and Marletta3, Reference Djordjević, Kim and Yoon7].) A subspace
![]() $\mathcal {M}\subseteq \mathcal {H}$
is called a nontrivial invariant subspace (NIS) of the pencil of
$\mathcal {M}\subseteq \mathcal {H}$
is called a nontrivial invariant subspace (NIS) of the pencil of
![]() $\mathbf {T}$
if
$\mathbf {T}$
if
![]() $\mathcal {M}\neq \left \{ 0\right \} ,\mathcal {H}$
and
$\mathcal {M}\neq \left \{ 0\right \} ,\mathcal {H}$
and
![]() $\mathbb {T}_{\lambda }\mathcal {M}\subseteq \mathcal {M}$
for any
$\mathbb {T}_{\lambda }\mathcal {M}\subseteq \mathcal {M}$
for any
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
In this paper, we introduce the spherical polar decomposition of the linear pencil of an ordered pair
![]() $\mathbf {T}=(T_{1},T_{2})$
and investigate nontrivial invariant subspaces between the generalized spherical Aluthge transform of the linear pencil of
$\mathbf {T}=(T_{1},T_{2})$
and investigate nontrivial invariant subspaces between the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}$
and the linear pencil of the original pair
$\mathbf {T}$
and the linear pencil of the original pair
![]() $\mathbf {T}$
of bounded operators with dense ranges. We briefly state our main results. In Theorem 1.5, we show that for a pair
$\mathbf {T}$
of bounded operators with dense ranges. We briefly state our main results. In Theorem 1.5, we show that for a pair
![]() $\mathbf {T}$
of operators with dense range and for
$\mathbf {T}$
of operators with dense range and for
![]() $0\leq t\leq 1$
, if the linear pencil of
$0\leq t\leq 1$
, if the linear pencil of
![]() $\mathbf {T}$
has an NIS, then the generalized spherical Aluthge transform of the linear pencil of
$\mathbf {T}$
has an NIS, then the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}$
has also an NIS. In Theorem 1.7, we show that the converse of the result in Theorem 1.5 is true when
$\mathbf {T}$
has also an NIS. In Theorem 1.7, we show that the converse of the result in Theorem 1.5 is true when
 $T=\left ( \begin {array}{c} T_{1} \\ T_{2} \end {array} \right ) $
is bounded below. Next, in Theorem 1.8, we show that for
$T=\left ( \begin {array}{c} T_{1} \\ T_{2} \end {array} \right ) $
is bounded below. Next, in Theorem 1.8, we show that for
![]() $0\leq t\leq 1$
,
$0\leq t\leq 1$
,
![]() $\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
has an NIS if and only if the generalized spherical Aluthge transform
$\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
has an NIS if and only if the generalized spherical Aluthge transform
![]() $\{ \widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
has an NIS, when
$\{ \widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
has an NIS, when
![]() $\mathbf {T}=(T_{1},T_{2})$
is a commuting pair of operators with dense ranges. Next, in Theorem 1.9, we can show that for
$\mathbf {T}=(T_{1},T_{2})$
is a commuting pair of operators with dense ranges. Next, in Theorem 1.9, we can show that for
![]() $ 0\leq t\leq 1$
,
$ 0\leq t\leq 1$
,
![]() $\widehat {\mathbf {T}^{t}}$
is a commuting pair and
$\widehat {\mathbf {T}^{t}}$
is a commuting pair and
![]() $\widehat { \mathbf {T}^{t}}$
has a nontrivial joint invariant subspace (NJIS) if and only if
$\widehat { \mathbf {T}^{t}}$
has a nontrivial joint invariant subspace (NJIS) if and only if
![]() $\mathbf {T}$
does, when
$\mathbf {T}$
does, when
![]() $\mathbf {T}=(T_{1},T_{2})$
is a commuting pair of operators with dense ranges. In Theorem 1.9, we first employ a tool and technique which connects a relation between an NJIS and NIS in multivariable and single operator theories to obtain a new proof of the known results in [Reference Djordjević, Kim and Yoon8, Reference Kim and Yoon12, Reference Kim and Yoon13]. Finally, in Example 1.11, we give a partial answer to Conjecture 1.10 in [Reference Kim and Yoon13, Conjecture 2.29].
$\mathbf {T}=(T_{1},T_{2})$
is a commuting pair of operators with dense ranges. In Theorem 1.9, we first employ a tool and technique which connects a relation between an NJIS and NIS in multivariable and single operator theories to obtain a new proof of the known results in [Reference Djordjević, Kim and Yoon8, Reference Kim and Yoon12, Reference Kim and Yoon13]. Finally, in Example 1.11, we give a partial answer to Conjecture 1.10 in [Reference Kim and Yoon13, Conjecture 2.29].
We now introduce some definitions and terminology for our paper. The polar decomposition of a bounded linear operator S in
![]() $\mathcal {B(H},\mathcal {K)} $
is a canonical factorization
$\mathcal {B(H},\mathcal {K)} $
is a canonical factorization
![]() $S=U\left \vert S\right \vert $
, where
$S=U\left \vert S\right \vert $
, where
![]() $ \left \vert S\right \vert =\sqrt {S^{\ast }S}$
is a positive operator, U is a partial isometry with
$ \left \vert S\right \vert =\sqrt {S^{\ast }S}$
is a positive operator, U is a partial isometry with
![]() $(\mathrm {ker}S)^{\perp }$
as its initial space and
$(\mathrm {ker}S)^{\perp }$
as its initial space and
![]() $ \overline {\mathrm {ran}S}$
, the closure of
$ \overline {\mathrm {ran}S}$
, the closure of
![]() $\mathrm {ran}S$
, as its final space, and
$\mathrm {ran}S$
, as its final space, and
![]() $\mathrm {ker}S=\mathrm {ker}U=\mathrm {ker}\left \vert S\right \vert $
. It is known that if
$\mathrm {ker}S=\mathrm {ker}U=\mathrm {ker}\left \vert S\right \vert $
. It is known that if
![]() $S=WP$
, where P is positive and W is a partial isometry with
$S=WP$
, where P is positive and W is a partial isometry with
![]() $\mathrm {ker}W=\mathrm {ker}P$
, then
$\mathrm {ker}W=\mathrm {ker}P$
, then
![]() $P=|S|$
and
$P=|S|$
and
![]() $U=W$
. The polar decomposition for the linear pencil of an ordered pair
$U=W$
. The polar decomposition for the linear pencil of an ordered pair
![]() $\mathbf {T} =(T_{1},T_{2})$
needs to be defined uniformly for all operators in
$\mathbf {T} =(T_{1},T_{2})$
needs to be defined uniformly for all operators in
![]() $\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. For this, we observe the polar decomposition for the operator T such that
$\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. For this, we observe the polar decomposition for the operator T such that
 $$ \begin{align*} T=\left( \begin{array}{c} T_{1} \\ T_{2} \end{array} \right) =VP:\mathcal{H}\rightarrow \mathcal{H}\oplus \mathcal{H}, \end{align*} $$
$$ \begin{align*} T=\left( \begin{array}{c} T_{1} \\ T_{2} \end{array} \right) =VP:\mathcal{H}\rightarrow \mathcal{H}\oplus \mathcal{H}, \end{align*} $$
where
![]() $T=VP$
is the polar decomposition of T,
$T=VP$
is the polar decomposition of T,
 $V=\left ( \begin {array}{c} V_{1} \\ V_{2} \end {array} \right ) $
is a partial isometry from
$V=\left ( \begin {array}{c} V_{1} \\ V_{2} \end {array} \right ) $
is a partial isometry from
![]() $\mathcal {H}$
to
$\mathcal {H}$
to
![]() $\mathcal {H}\oplus \mathcal {H}$
, and
$\mathcal {H}\oplus \mathcal {H}$
, and
![]() $P=\left \vert T\right \vert =\left ( T^{\ast }T\right ) ^{ \frac {1}{2}}=\left ( T_{1}^{\ast }T_{1}+T_{2}^{\ast }T_{2}\right ) ^{\frac {1}{2 }}$
is the positive operator on
$P=\left \vert T\right \vert =\left ( T^{\ast }T\right ) ^{ \frac {1}{2}}=\left ( T_{1}^{\ast }T_{1}+T_{2}^{\ast }T_{2}\right ) ^{\frac {1}{2 }}$
is the positive operator on
![]() $\mathcal {H}$
(see [Reference Curto and Yoon5, Reference Curto and Yoon6, Reference Kim and Yoon12, Reference Kim and Yoon13]). Now we define the polar decomposition of the linear pencil of an ordered pair
$\mathcal {H}$
(see [Reference Curto and Yoon5, Reference Curto and Yoon6, Reference Kim and Yoon12, Reference Kim and Yoon13]). Now we define the polar decomposition of the linear pencil of an ordered pair
![]() $\mathbf {T}=(T_{1},T_{2})$
by using the polar decomposition of T in
$\mathbf {T}=(T_{1},T_{2})$
by using the polar decomposition of T in
![]() $\mathcal {B(H},\mathcal {H}\oplus \mathcal {H)}$
.
$\mathcal {B(H},\mathcal {H}\oplus \mathcal {H)}$
.
Definition 1.1 The polar decomposition of the linear pencil of an ordered pair
![]() $\mathbf {T}\,{=}\, (T_{1},T_{2})$
is the linear pencil of the ordered pair
$\mathbf {T}\,{=}\, (T_{1},T_{2})$
is the linear pencil of the ordered pair
![]() $(V_{1}P,V_{2}P)$
, i.e.,
$(V_{1}P,V_{2}P)$
, i.e.,
Recall the Aluthge transform
![]() $\widetilde {S}:=|S|^{\frac {1}{2}}U|S|^{ \frac {1}{2}}$
, the generalized Aluthge transform
$\widetilde {S}:=|S|^{\frac {1}{2}}U|S|^{ \frac {1}{2}}$
, the generalized Aluthge transform
![]() $\widetilde {S^{t}} :=|S|^{t}U|S|^{1-t}$
(
$\widetilde {S^{t}} :=|S|^{t}U|S|^{1-t}$
(
![]() $0\leq t\leq 1$
), and the Duggal transform
$0\leq t\leq 1$
), and the Duggal transform
![]() $ \widetilde {S}^{D}:=|S|U$
of
$ \widetilde {S}^{D}:=|S|U$
of
![]() $S=U\left \vert S\right \vert \in \mathcal {B}( \mathcal {H})$
. These transformations have received considerable attention in recent years. For more details, the reader is referred to [Reference Aluthge1, Reference Benhida, Curto, Lee and Yoon2, Reference Cho, Jung and Lee4, Reference Ito, Yamazaki and Yanagida10, Reference Jung, Ko and Pearcy11, Reference Kim and Yoon13].
$S=U\left \vert S\right \vert \in \mathcal {B}( \mathcal {H})$
. These transformations have received considerable attention in recent years. For more details, the reader is referred to [Reference Aluthge1, Reference Benhida, Curto, Lee and Yoon2, Reference Cho, Jung and Lee4, Reference Ito, Yamazaki and Yanagida10, Reference Jung, Ko and Pearcy11, Reference Kim and Yoon13].
Let
![]() $\mathbf {T}=(T_{1},T_{2})\equiv (V_{1}P,V_{2}P)$
be a pair of operators, where P,
$\mathbf {T}=(T_{1},T_{2})\equiv (V_{1}P,V_{2}P)$
be a pair of operators, where P,
![]() $V_{1}$
, and
$V_{1}$
, and
![]() $V_{2}$
are given above. Naturally, we can get the spherical polar decomposition of a pair of operators
$V_{2}$
are given above. Naturally, we can get the spherical polar decomposition of a pair of operators
![]() $\mathbf {T} =(T_{1},T_{2})$
as follows [Reference Kim and Yoon12, Reference Kim and Yoon13]:
$\mathbf {T} =(T_{1},T_{2})$
as follows [Reference Kim and Yoon12, Reference Kim and Yoon13]:
Then, for
![]() $0\leq t\leq 1$
, the generalized spherical Aluthge transform
$0\leq t\leq 1$
, the generalized spherical Aluthge transform
![]() $\widehat {\mathbf {T}^{t}}$
is defined by
$\widehat {\mathbf {T}^{t}}$
is defined by
In particular, when
![]() $t=\frac {1}{2}$
(resp.
$t=\frac {1}{2}$
(resp.
![]() $t=1$
), we call the spherical Aluthge (resp. Duggal) transform
$t=1$
), we call the spherical Aluthge (resp. Duggal) transform
![]() $\widehat {\mathbf {T}}$
(resp.
$\widehat {\mathbf {T}}$
(resp.
![]() $\widehat {\mathbf {T}}^{D}$
) of
$\widehat {\mathbf {T}}^{D}$
) of
![]() $\mathbf {T}$
, that is,
$\mathbf {T}$
, that is,
Now we define the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}=(T_{1},T_{2})$
.
$\mathbf {T}=(T_{1},T_{2})$
.
Definition 1.2 For
![]() $0\leq t\leq 1$
, the generalized spherical Aluthge transform of the linear pencil of
$0\leq t\leq 1$
, the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}=(T_{1},T_{2})$
is defined as the linear pencil of
$\mathbf {T}=(T_{1},T_{2})$
is defined as the linear pencil of
![]() $\widehat {\mathbf {T}^{t}}=(\widehat {T_{1}^{t}},\widehat {T_{2}^{t}})$
, that is,
$\widehat {\mathbf {T}^{t}}=(\widehat {T_{1}^{t}},\widehat {T_{2}^{t}})$
, that is,
Also, the generalized spherical Aluthge transform
![]() $\widehat {\mathbb {T}} _{\lambda }^{t}$
at
$\widehat {\mathbb {T}} _{\lambda }^{t}$
at
![]() $\lambda \in \mathbb {C}$
of the linear pencil of
$\lambda \in \mathbb {C}$
of the linear pencil of
![]() $ \mathbf {T}= (T_{1},T_{2})$
is defined by
$ \mathbf {T}= (T_{1},T_{2})$
is defined by
When
![]() $t=\frac {1}{2}$
(resp.
$t=\frac {1}{2}$
(resp.
![]() $t=1$
), we will denote
$t=1$
), we will denote
![]() $\widehat {\mathbb {T}} _{\lambda }\equiv \widehat {\mathbb {T}}_{\lambda }^{\frac {1}{2}}$
(resp.
$\widehat {\mathbb {T}} _{\lambda }\equiv \widehat {\mathbb {T}}_{\lambda }^{\frac {1}{2}}$
(resp.
![]() $ \widehat {\mathbb {T}}_{\lambda }^{D}\equiv \widehat {\mathbb {T}}_{\lambda }^{1} $
) and call the spherical Aluthge transform (resp. the spherical Duggal transform) of the linear pencil of
$ \widehat {\mathbb {T}}_{\lambda }^{D}\equiv \widehat {\mathbb {T}}_{\lambda }^{1} $
) and call the spherical Aluthge transform (resp. the spherical Duggal transform) of the linear pencil of
![]() $\mathbf {T} =(T_{1},T_{2})$
at
$\mathbf {T} =(T_{1},T_{2})$
at
![]() $\lambda $
, i.e.,
$\lambda $
, i.e.,
It is known that the Aluthge transform has a natural connection with the invariant subspace problem, because every normal operator has nontrivial invariant subspaces and Aluthge transform is to convert an operator into another operator which shares with the first one many spectral properties, but which is closer to being a normal operator. However, for an infinite-dimensional Hilbert space
![]() $\mathcal {H}$
, one needs to remember the classical example of Exner in [Reference Exner9], who proved that, even for weighted shifts, subnormality is not preserved by the Aluthge transform; in this case, the transformed shift is farther from normal than the original one. In recent years, Jung, Ko, and Pearcy proved in [Reference Jung, Ko and Pearcy11] that an operator
$\mathcal {H}$
, one needs to remember the classical example of Exner in [Reference Exner9], who proved that, even for weighted shifts, subnormality is not preserved by the Aluthge transform; in this case, the transformed shift is farther from normal than the original one. In recent years, Jung, Ko, and Pearcy proved in [Reference Jung, Ko and Pearcy11] that an operator
![]() $S\in \mathcal {B}(\mathcal {H})$
with dense range has a nontrivial invariant subspace if and only if
$S\in \mathcal {B}(\mathcal {H})$
with dense range has a nontrivial invariant subspace if and only if
![]() $\widetilde {S}$
does. In [Reference Djordjević, Kim and Yoon8, Reference Kim and Yoon12, Reference Kim and Yoon13], the authors extended the above result to the generalized Aluthge transform and the generalized spherical Aluthge transform for commuting pairs of operators. We now consider a relation between the invariant subspaces for the linear pencil of
$\widetilde {S}$
does. In [Reference Djordjević, Kim and Yoon8, Reference Kim and Yoon12, Reference Kim and Yoon13], the authors extended the above result to the generalized Aluthge transform and the generalized spherical Aluthge transform for commuting pairs of operators. We now consider a relation between the invariant subspaces for the linear pencil of
![]() $\mathbf {T} =(T_{1},T_{2})$
and those for the linear pencil of its generalized Aluthge transform.
$\mathbf {T} =(T_{1},T_{2})$
and those for the linear pencil of its generalized Aluthge transform.
We let
![]() $\mathrm {Lat}(S)$
be the set of common invariant subspaces for S. First, we have the following.
$\mathrm {Lat}(S)$
be the set of common invariant subspaces for S. First, we have the following.
Proposition 1.3 Let
![]() $\mathbf {T}=(T_{1},T_{2})$
be a pair of operators. Then
$\mathbf {T}=(T_{1},T_{2})$
be a pair of operators. Then
![]() $ \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} = \mathrm {Lat}T_{1}\cap \mathrm {Lat}T_{2}$
.
$ \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} = \mathrm {Lat}T_{1}\cap \mathrm {Lat}T_{2}$
.
Proof
![]() $\left ( \subseteq \right ) :$
Let
$\left ( \subseteq \right ) :$
Let
![]() $\mathcal {M}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. Then
$\mathcal {M}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. Then
![]() $\left ( T_{1}-0\cdot T_{2}\right ) \left ( \mathcal {M}\right ) \subseteq \mathcal {M}$
, i.e.,
$\left ( T_{1}-0\cdot T_{2}\right ) \left ( \mathcal {M}\right ) \subseteq \mathcal {M}$
, i.e.,
![]() $T_{1}\mathcal {M}\subseteq \mathcal {M}$
. Let
$T_{1}\mathcal {M}\subseteq \mathcal {M}$
. Let
![]() $x\in \mathcal {M}$
. Then
$x\in \mathcal {M}$
. Then
![]() $ \left ( T_{1}-\lambda T_{2}\right ) x\in \mathcal {M}$
for all
$ \left ( T_{1}-\lambda T_{2}\right ) x\in \mathcal {M}$
for all
![]() $\lambda \in \mathbb {C}$
, which implies that
$\lambda \in \mathbb {C}$
, which implies that
![]() $\left ( \frac {1}{\lambda }T_{1}-T_{2}\right ) x\in \mathcal {M}$
for all
$\left ( \frac {1}{\lambda }T_{1}-T_{2}\right ) x\in \mathcal {M}$
for all
![]() $\lambda \neq 0$
. Since
$\lambda \neq 0$
. Since
![]() $\mathcal {M}$
is closed, letting
$\mathcal {M}$
is closed, letting
![]() $\lambda \rightarrow \infty $
,
$\lambda \rightarrow \infty $
,
![]() $-T_{2}x\in \mathcal {M}$
, i.e.,
$-T_{2}x\in \mathcal {M}$
, i.e.,
![]() $ T_{2}x\in \mathcal {M}$
. Thus,
$ T_{2}x\in \mathcal {M}$
. Thus,
![]() $T_{2}\mathcal {M}\subseteq \mathcal {M}$
. Therefore, we have that
$T_{2}\mathcal {M}\subseteq \mathcal {M}$
. Therefore, we have that
![]() $\mathcal {M}\in \mathrm {Lat}T_{1}\cap \mathrm {Lat} T_{2}$
.
$\mathcal {M}\in \mathrm {Lat}T_{1}\cap \mathrm {Lat} T_{2}$
.
![]() $\left ( \supseteq \right ) :$
Let
$\left ( \supseteq \right ) :$
Let
![]() $\mathcal {N}\in \mathrm {Lat}T_{1}\cap \mathrm {Lat}T_{2}$
. Then
$\mathcal {N}\in \mathrm {Lat}T_{1}\cap \mathrm {Lat}T_{2}$
. Then
![]() $T_{1}\mathcal {N}\subseteq \mathcal {N}$
and
$T_{1}\mathcal {N}\subseteq \mathcal {N}$
and
![]() $T_{2} \mathcal {N}\subseteq \mathcal {N}$
. Let
$T_{2} \mathcal {N}\subseteq \mathcal {N}$
. Let
![]() $x\in \mathcal {N}$
. Then
$x\in \mathcal {N}$
. Then
![]() $ T_{1}x,T_{2}x\in \mathcal {N}$
. So
$ T_{1}x,T_{2}x\in \mathcal {N}$
. So
![]() $\left ( T_{1}-\lambda T_{2}\right ) x\in \mathcal {N}$
, i.e.,
$\left ( T_{1}-\lambda T_{2}\right ) x\in \mathcal {N}$
, i.e.,
![]() $\left ( T_{1}-\lambda T_{2}\right ) \left ( \mathcal {N} \right ) \subseteq \mathcal {N}$
for all
$\left ( T_{1}-\lambda T_{2}\right ) \left ( \mathcal {N} \right ) \subseteq \mathcal {N}$
for all
![]() $\lambda \in \mathbb {C}$
. Therefore,
$\lambda \in \mathbb {C}$
. Therefore,
![]() $ \mathcal {N}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C} \right \} $
.
$ \mathcal {N}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C} \right \} $
.
Proposition 1.4 For a pair of operators
![]() $\mathbf {T} =(T_{1},T_{2})=(V_{1}P,V_{2}P)$
and
$\mathbf {T} =(T_{1},T_{2})=(V_{1}P,V_{2}P)$
and
![]() $0\leq t\leq 1$
, we have:
$0\leq t\leq 1$
, we have:
-
(i)
 $P^{t}\mathbb {T}_{\lambda }=\widehat {\mathbb {T}}_{\lambda }^{t}P^{t}$
for
$P^{t}\mathbb {T}_{\lambda }=\widehat {\mathbb {T}}_{\lambda }^{t}P^{t}$
for
 $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
. -
(ii)
 $(V_{1}-\lambda V_{2})P^{1-t}\widehat {\mathbb {T}}_{\lambda }^{t}= \mathbb {T}_{\lambda }(V_{1}-\lambda V_{2})P^{1-t}$
for
$(V_{1}-\lambda V_{2})P^{1-t}\widehat {\mathbb {T}}_{\lambda }^{t}= \mathbb {T}_{\lambda }(V_{1}-\lambda V_{2})P^{1-t}$
for
 $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
Proof (i) and (ii) are clear from direct calculations.
Next, we study nontrivial invariant subspaces between the linear pencil of
![]() $\mathbf {T}$
and the linear pencil of its generalized Aluthge transform.
$\mathbf {T}$
and the linear pencil of its generalized Aluthge transform.
Theorem 1.5 Let
![]() $\mathbf {T}=(T_{1},T_{2})$
be a pair of operators with dense range. For
$\mathbf {T}=(T_{1},T_{2})$
be a pair of operators with dense range. For
![]() $0\leq t<1$
, we have that if the linear pencil of
$0\leq t<1$
, we have that if the linear pencil of
![]() $ \mathbf {T}$
has an NIS, then the generalized spherical Aluthge transform of the linear pencil of
$ \mathbf {T}$
has an NIS, then the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}$
has an NIS.
$\mathbf {T}$
has an NIS.
Proof For
![]() $t=0$
, the desired one is clear.
$t=0$
, the desired one is clear.
For
![]() $0<t<1$
, suppose that
$0<t<1$
, suppose that
![]() $\mathrm {ker}P\neq \left \{ 0\right \} $
. Then
$\mathrm {ker}P\neq \left \{ 0\right \} $
. Then
![]() $ \mathrm {ker}P\neq \mathcal {H}$
, because
$ \mathrm {ker}P\neq \mathcal {H}$
, because
![]() $T_{1}\neq 0$
and
$T_{1}\neq 0$
and
![]() $T_{2}\neq 0$
. Since
$T_{2}\neq 0$
. Since
![]() $\mathrm {ker}P=\mathrm {ker}T_{1}\cap \mathrm {ker}T_{2}={\bigcap } _{\lambda \in \mathbb {C}}\mathrm {ker}(T_{1}-\lambda T_{2})$
,
$\mathrm {ker}P=\mathrm {ker}T_{1}\cap \mathrm {ker}T_{2}={\bigcap } _{\lambda \in \mathbb {C}}\mathrm {ker}(T_{1}-\lambda T_{2})$
,
![]() $\mathrm {ker} P\in \mathrm {Lat}T_{1}\cap \mathrm {Lat}T_{2}$
, and by Proposition 1.3,
$\mathrm {ker} P\in \mathrm {Lat}T_{1}\cap \mathrm {Lat}T_{2}$
, and by Proposition 1.3,
![]() $\mathrm {ker}P\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, i.e., the linear pencil of
$\mathrm {ker}P\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, i.e., the linear pencil of
![]() $\mathbf {T}$
has a nontrivial invariant subspace. On the other hand, since
$\mathbf {T}$
has a nontrivial invariant subspace. On the other hand, since
![]() $\mathrm {ker} P^{1-t}=\mathrm {ker}P\neq \left \{ 0\right \} ,\mathcal {H}$
and
$\mathrm {ker} P^{1-t}=\mathrm {ker}P\neq \left \{ 0\right \} ,\mathcal {H}$
and
![]() $\mathrm {ker} P^{1-t}\in \mathrm {Lat}\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}} :\lambda \in \mathbb {C\}}$
, the generalized spherical Aluthge transform of the linear pencil of
$\mathrm {ker} P^{1-t}\in \mathrm {Lat}\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}} :\lambda \in \mathbb {C\}}$
, the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}$
has a nontrivial invariant subspace. So, we may assume that
$\mathbf {T}$
has a nontrivial invariant subspace. So, we may assume that
![]() $\mathrm {ker}P=\left \{ 0\right \} $
. Let
$\mathrm {ker}P=\left \{ 0\right \} $
. Let
![]() $\mathcal {M}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
be nontrivial. Consider
$\mathcal {M}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
be nontrivial. Consider
![]() $\mathcal {N}=\overline {P^{t}\mathcal {M}}$
, where
$\mathcal {N}=\overline {P^{t}\mathcal {M}}$
, where
![]() $ \overline {P^{t}\mathcal {M}}$
means the smallest closed set containing
$ \overline {P^{t}\mathcal {M}}$
means the smallest closed set containing
![]() $P^{t} \mathcal {M}$
. Since
$P^{t} \mathcal {M}$
. Since
![]() $\mathrm {ker}P=\left \{ 0\right \} $
, we have
$\mathrm {ker}P=\left \{ 0\right \} $
, we have
![]() $\mathcal {N }\neq \left \{ 0\right \} $
. Suppose that
$\mathcal {N }\neq \left \{ 0\right \} $
. Suppose that
![]() $\mathcal {N}=\mathcal {H}$
, i.e.,
$\mathcal {N}=\mathcal {H}$
, i.e.,
![]() $ \overline {P^{t}\mathcal {M}}=\mathcal {H}$
. Since
$ \overline {P^{t}\mathcal {M}}=\mathcal {H}$
. Since
![]() $T_{i} \left ( i=1,2\right ) $
has dense range,
$T_{i} \left ( i=1,2\right ) $
has dense range,
![]() $V_{i} \left ( i=1,2\right ) $
also has dense range. Since
$V_{i} \left ( i=1,2\right ) $
also has dense range. Since
![]() $\mathrm {ker}P^{1-t}=\mathrm {ker}P=\left \{ 0\right \} $
,
$\mathrm {ker}P^{1-t}=\mathrm {ker}P=\left \{ 0\right \} $
,
![]() $P^{1-t}$
has dense range, and so
$P^{1-t}$
has dense range, and so
![]() $V_{i}P^{1-t}$
has dense range. Thus, we have that
$V_{i}P^{1-t}$
has dense range. Thus, we have that
which is a contradiction. Hence,
![]() $\mathcal {N}\neq \mathcal {H}$
, which means that
$\mathcal {N}\neq \mathcal {H}$
, which means that
![]() $\mathcal {N}$
is nontrivial. Now, by Proposition 1.4(i), note that, for
$\mathcal {N}$
is nontrivial. Now, by Proposition 1.4(i), note that, for
![]() $\lambda \in \mathbb {C}$
,
$\lambda \in \mathbb {C}$
,
Therefore,
![]() $\mathcal {N}\in \mathrm {Lat}\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
and we have the desired one.
$\mathcal {N}\in \mathrm {Lat}\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
and we have the desired one.
For
![]() $t=1$
, by the proof of the case for
$t=1$
, by the proof of the case for
![]() $0<t<1$
, we can assume that
$0<t<1$
, we can assume that
![]() $\mathrm { ker}P=\left \{ 0\right \} $
. Next, for a nontrivial
$\mathrm { ker}P=\left \{ 0\right \} $
. Next, for a nontrivial
![]() $\mathcal {M}$
in
$\mathcal {M}$
in
![]() $ \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, we consider
$ \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, we consider
![]() $\mathcal {L}=\overline {P\mathcal {M}}$
. Then
$\mathcal {L}=\overline {P\mathcal {M}}$
. Then
![]() $\mathcal {L}\neq \left \{ 0\right \} $
. Suppose that
$\mathcal {L}\neq \left \{ 0\right \} $
. Suppose that
![]() $\mathcal {L}=\mathcal {H}$
, i.e.,
$\mathcal {L}=\mathcal {H}$
, i.e.,
![]() $ \overline {P\mathcal {M}}=\mathcal {H}$
. Since
$ \overline {P\mathcal {M}}=\mathcal {H}$
. Since
![]() $V_{i} \left ( i=1,2\right ) $
also has dense range, by (1.1) when
$V_{i} \left ( i=1,2\right ) $
also has dense range, by (1.1) when
![]() $t=1$
, we have that
$t=1$
, we have that
which is also a contradiction. Hence,
![]() $\mathcal {L}$
is nontrivial. Now, by Proposition 1.4(i), note that, for
$\mathcal {L}$
is nontrivial. Now, by Proposition 1.4(i), note that, for
![]() $\lambda \in \mathbb {C}$
,
$\lambda \in \mathbb {C}$
,
Therefore,
![]() $\mathcal {N}\in \mathrm {Lat}\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
and our proof is now completed.
$\mathcal {N}\in \mathrm {Lat}\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
and our proof is now completed.
The converse of the result in Theorem 1.5 is true when
 $T=\left ( \begin {array}{c} T_{1} \\ T_{2} \end {array} \right ) =VP=\left ( \begin {array}{c} V_{1} \\ V_{2} \end {array} \right ) P$
is bounded below, i.e., if T is bounded below, then we have that the linear pencil of
$T=\left ( \begin {array}{c} T_{1} \\ T_{2} \end {array} \right ) =VP=\left ( \begin {array}{c} V_{1} \\ V_{2} \end {array} \right ) P$
is bounded below, i.e., if T is bounded below, then we have that the linear pencil of
![]() $\mathbf {T}$
has an NIS if and only if the generalized spherical Aluthge transform of the linear pencil of
$\mathbf {T}$
has an NIS if and only if the generalized spherical Aluthge transform of the linear pencil of
![]() $\mathbf {T}$
has an NIS. For this, we first consider the following.
$\mathbf {T}$
has an NIS. For this, we first consider the following.
Proposition 1.6 If T is bounded below, then P is invertible.
Proof Since T is bounded below, there exists
![]() $c>0$
such that
$c>0$
such that
![]() $\Vert Tx\Vert =\left \Vert VPx\right \Vert \geq c\left \Vert x\right \Vert $
for all
$\Vert Tx\Vert =\left \Vert VPx\right \Vert \geq c\left \Vert x\right \Vert $
for all
![]() $x\in \mathcal {H}$
. Thus, for all
$x\in \mathcal {H}$
. Thus, for all
![]() $x\in \mathcal {H}$
,
$x\in \mathcal {H}$
,
 $$ \begin{align*} \begin{array}{l} \left\Vert VPx\right\Vert \geq c\left\Vert x\right\Vert \Longrightarrow \left\Vert V\right\Vert \left\Vert Px\right\Vert \geq c\left\Vert x\right\Vert \\ \overset{V\text{ is a partial isometry}}{\Longrightarrow }\left\Vert Px\right\Vert \geq c\left\Vert x\right\Vert{\kern-2pt}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \left\Vert VPx\right\Vert \geq c\left\Vert x\right\Vert \Longrightarrow \left\Vert V\right\Vert \left\Vert Px\right\Vert \geq c\left\Vert x\right\Vert \\ \overset{V\text{ is a partial isometry}}{\Longrightarrow }\left\Vert Px\right\Vert \geq c\left\Vert x\right\Vert{\kern-2pt}. \end{array} \end{align*} $$
Therefore, P is bounded below. Since P is positive, P is invertible, as desired.
Now we have the following.
Theorem 1.7 Let T be bounded below. Then, for
![]() $0\leq t\leq 1$
, we have that the linear pencil
$0\leq t\leq 1$
, we have that the linear pencil
![]() $\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C} \right \} $
has an NIS if and only if the generalized spherical Aluthge transform
$\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C} \right \} $
has an NIS if and only if the generalized spherical Aluthge transform
has an NIS.
Proof
![]() $\left ( \Longrightarrow \right ) $
It is clear from Theorem 1.5.
$\left ( \Longrightarrow \right ) $
It is clear from Theorem 1.5.
![]() $\left ( \Longleftarrow \right ) $
For
$\left ( \Longleftarrow \right ) $
For
![]() $t=0$
, the desired one is clear.
$t=0$
, the desired one is clear.
For
![]() $0<t\leq 1$
, let
$0<t\leq 1$
, let
![]() $\mathcal {N}\in \mathrm {Lat}\{\widehat {T_{1}^{t}} -\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
be nontrivial. Since T is bounded below, by Proposition 1.6, P is invertible. So,
$\mathcal {N}\in \mathrm {Lat}\{\widehat {T_{1}^{t}} -\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
be nontrivial. Since T is bounded below, by Proposition 1.6, P is invertible. So,
![]() $\mathcal {R}=P^{-t}\mathcal {N}$
is nontrivial and closed. Since
$\mathcal {R}=P^{-t}\mathcal {N}$
is nontrivial and closed. Since
![]() $ \widehat {\mathbb {T}}_{\lambda }^{t}\mathcal {N}\subset \mathcal {N}$
, we have that
$ \widehat {\mathbb {T}}_{\lambda }^{t}\mathcal {N}\subset \mathcal {N}$
, we have that
![]() $P^{t}(V_{1}-\lambda V_{2})P^{1-t}\mathcal {N}\subset \mathcal {N}$
. Since
$P^{t}(V_{1}-\lambda V_{2})P^{1-t}\mathcal {N}\subset \mathcal {N}$
. Since
![]() $P^{t}$
is invertible,
$P^{t}$
is invertible,
![]() $(V_{1}-\lambda V_{2})P^{1-t}\mathcal {N}\subset P^{-t}\mathcal {N}$
, and so
$(V_{1}-\lambda V_{2})P^{1-t}\mathcal {N}\subset P^{-t}\mathcal {N}$
, and so
![]() $(V_{1}-\lambda V_{2})P\left ( P^{-t}\mathcal {N} \right ) \subset P^{-t}\mathcal {N}$
, i.e.,
$(V_{1}-\lambda V_{2})P\left ( P^{-t}\mathcal {N} \right ) \subset P^{-t}\mathcal {N}$
, i.e.,
![]() $\mathbb {T}_{\lambda }\mathcal {R} \subset \mathcal {R}$
. Therefore, the linear pencil
$\mathbb {T}_{\lambda }\mathcal {R} \subset \mathcal {R}$
. Therefore, the linear pencil
![]() $\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
has an NIS, as desired.
$\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
has an NIS, as desired.
Theorem 1.8 Let
![]() $\mathbf {T}=(T_{1},T_{2})$
be a commuting pair of operators with dense ranges. Then, for
$\mathbf {T}=(T_{1},T_{2})$
be a commuting pair of operators with dense ranges. Then, for
![]() $0\leq t\leq 1$
, the linear pencil
$0\leq t\leq 1$
, the linear pencil
![]() $ \left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
has an NIS if and only if the generalized spherical Aluthge transform
$ \left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
has an NIS if and only if the generalized spherical Aluthge transform
![]() $\{\widehat {T_{1}^{t} }-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
has an NIS.
$\{\widehat {T_{1}^{t} }-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
has an NIS.
Proof
![]() $\left ( \Longrightarrow \right ) $
It is clear from Theorem 1.5.
$\left ( \Longrightarrow \right ) $
It is clear from Theorem 1.5.
![]() $\left ( \Longleftarrow \right ) $
Suppose that
$\left ( \Longleftarrow \right ) $
Suppose that
![]() $\mathrm {ker}T_{1}\neq \left \{ 0\right \} $
. Since
$\mathrm {ker}T_{1}\neq \left \{ 0\right \} $
. Since
![]() $\mathbf {T}=(T_{1},T_{2})$
is a commuting pair of operators, for all
$\mathbf {T}=(T_{1},T_{2})$
is a commuting pair of operators, for all
![]() $x\in \mathrm {ker}T_{1}$
,
$x\in \mathrm {ker}T_{1}$
,
![]() $T_{1}\left ( T_{2}x\right ) =T_{2}\left ( T_{1}x\right ) =0$
. So
$T_{1}\left ( T_{2}x\right ) =T_{2}\left ( T_{1}x\right ) =0$
. So
![]() $T_{2}\left ( \mathrm {ker}T_{1}\right ) \subseteq \mathrm {ker}T_{1}$
. Hence,
$T_{2}\left ( \mathrm {ker}T_{1}\right ) \subseteq \mathrm {ker}T_{1}$
. Hence,
![]() $\left ( T_{1}-\lambda T_{2}\right ) \left ( \mathrm {ker}T_{1}\right ) \subseteq \mathrm {ker}T_{1}$
for all
$\left ( T_{1}-\lambda T_{2}\right ) \left ( \mathrm {ker}T_{1}\right ) \subseteq \mathrm {ker}T_{1}$
for all
![]() $ \lambda \in \mathbb {C}$
and
$ \lambda \in \mathbb {C}$
and
![]() $\mathrm {ker}T_{1}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. Similarly, if
$\mathrm {ker}T_{1}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. Similarly, if
![]() $ \mathrm {ker}T_{2}\neq \left \{ 0\right \} $
, then
$ \mathrm {ker}T_{2}\neq \left \{ 0\right \} $
, then
![]() $\mathrm {ker}T_{2}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. Thus, we may assume that
$\mathrm {ker}T_{2}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
. Thus, we may assume that
![]() $T_{1}$
and
$T_{1}$
and
![]() $T_{2}$
are both quasiaffinities.
$T_{2}$
are both quasiaffinities.
For
![]() $t=0$
, the desired one is clear.
$t=0$
, the desired one is clear.
For
![]() $0<t\leq 1$
, let
$0<t\leq 1$
, let
![]() $\mathcal {M}$
be an NIS for the linear pencil of the generalized spherical Aluthge transform
$\mathcal {M}$
be an NIS for the linear pencil of the generalized spherical Aluthge transform
![]() $\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
. Let
$\{\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
. Let
![]() $\mathcal {L}=\overline { V_{1}PV_{2}P^{1-t}\mathcal {M}}$
. Then
$\mathcal {L}=\overline { V_{1}PV_{2}P^{1-t}\mathcal {M}}$
. Then
![]() $\mathcal {L}\neq \mathcal {H}$
. Indeed, if so, then
$\mathcal {L}\neq \mathcal {H}$
. Indeed, if so, then
![]() $P^{t}\mathcal {L}$
is dense in
$P^{t}\mathcal {L}$
is dense in
![]() $\mathcal {H}$
, since
$\mathcal {H}$
, since
Let
![]() $x\in V_{1}PV_{2}P^{1-t}\mathcal {M}$
with
$x\in V_{1}PV_{2}P^{1-t}\mathcal {M}$
with
![]() $x\neq 0$
. Then there is
$x\neq 0$
. Then there is
![]() $ z\in \mathcal {M}$
such that
$ z\in \mathcal {M}$
such that
![]() $x=V_{1}PV_{2}P^{1-t}z$
. Since
$x=V_{1}PV_{2}P^{1-t}z$
. Since
![]() $z\in \mathcal {M }$
,
$z\in \mathcal {M }$
,
![]() $(\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}})z\in \mathcal {M}$
, which means that
$(\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}})z\in \mathcal {M}$
, which means that
![]() $(\frac {1}{\lambda }\widehat {T_{1}^{t}}-\widehat {T_{2}^{t}} )z\in \mathcal {M}$
for
$(\frac {1}{\lambda }\widehat {T_{1}^{t}}-\widehat {T_{2}^{t}} )z\in \mathcal {M}$
for
![]() $\lambda \neq 0$
. Letting
$\lambda \neq 0$
. Letting
![]() $\lambda \rightarrow \infty $
, we have that
$\lambda \rightarrow \infty $
, we have that
![]() $\widehat {T_{2}^{t}}z\in \mathcal {M}$
. Of course,
$\widehat {T_{2}^{t}}z\in \mathcal {M}$
. Of course,
![]() $ \widehat {T_{1}^{t}}z\in \mathcal {M}$
when
$ \widehat {T_{1}^{t}}z\in \mathcal {M}$
when
![]() $\lambda =0$
. Since
$\lambda =0$
. Since
![]() $\widehat { T_{2}^{t}}z\in \mathcal {M}$
,
$\widehat { T_{2}^{t}}z\in \mathcal {M}$
,
![]() $(\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t} })(\widehat {T_{2}^{t}}z)\in \mathcal {M}$
for all
$(\widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t} })(\widehat {T_{2}^{t}}z)\in \mathcal {M}$
for all
![]() $\lambda \in \mathbb {C}$
. Thus, we have that
$\lambda \in \mathbb {C}$
. Thus, we have that
Consider
![]() $P^{t}x$
. Then, by (1.3), we have
$P^{t}x$
. Then, by (1.3), we have
So, by (1.4), we have
![]() $P^{t}\mathcal {L}\subseteq \mathcal {M}\neq \mathcal {H}$
, which contradicts to the fact that
$P^{t}\mathcal {L}\subseteq \mathcal {M}\neq \mathcal {H}$
, which contradicts to the fact that
![]() $\overline {P^{t}\mathcal {L}}= \mathcal {H}$
.
$\overline {P^{t}\mathcal {L}}= \mathcal {H}$
.
Also,
![]() $\mathcal {L}\neq \left \{ 0\right \} $
. Indeed, if so,
$\mathcal {L}\neq \left \{ 0\right \} $
. Indeed, if so,
![]() $ V_{1}PV_{2}P^{1-t}z=0$
for a nonzero vector
$ V_{1}PV_{2}P^{1-t}z=0$
for a nonzero vector
![]() $z\in \mathcal {M}$
. Since
$z\in \mathcal {M}$
. Since
![]() $ V_{1}PV_{2}P^{1-t}z=T_{1}\left ( V_{2}P^{1-t}z\right ) =0$
, we have
$ V_{1}PV_{2}P^{1-t}z=T_{1}\left ( V_{2}P^{1-t}z\right ) =0$
, we have
![]() $ V_{2}P^{1-t}z=0$
because of the quasiaffinity of
$ V_{2}P^{1-t}z=0$
because of the quasiaffinity of
![]() $T_{1}$
. Thus, we have that
$T_{1}$
. Thus, we have that
![]() $P^{1-t}z\in \mathrm {ker}V_{2}$
. On the other hand, since
$P^{1-t}z\in \mathrm {ker}V_{2}$
. On the other hand, since
![]() $T_{1}$
and
$T_{1}$
and
![]() $T_{2}$
are commuting,
$T_{2}$
are commuting,
![]() $V_{1}PV_{2}=V_{2}PV_{1}$
. Hence,
$V_{1}PV_{2}=V_{2}PV_{1}$
. Hence,
![]() $ V_{1}PV_{2}P^{1-t}z=V_{2}PV_{1}P^{1-t}z=T_{2}\left ( V_{1}P^{1-t}z\right ) =0$
, so
$ V_{1}PV_{2}P^{1-t}z=V_{2}PV_{1}P^{1-t}z=T_{2}\left ( V_{1}P^{1-t}z\right ) =0$
, so
![]() $V_{1}P^{1-t}z=0$
, i.e.,
$V_{1}P^{1-t}z=0$
, i.e.,
![]() $P^{1-t}z\in \mathrm {ker}V_{1}$
. Therefore,
$P^{1-t}z\in \mathrm {ker}V_{1}$
. Therefore,
![]() $ P^{1-t}z\in \mathrm {ker}V_{1}\cap \mathrm {ker}V_{2}=\left \{ 0\right \} $
. Since
$ P^{1-t}z\in \mathrm {ker}V_{1}\cap \mathrm {ker}V_{2}=\left \{ 0\right \} $
. Since
![]() $\mathrm {ker}P^{1-t}=\left \{ 0\right \} $
,
$\mathrm {ker}P^{1-t}=\left \{ 0\right \} $
,
![]() $z=0$
, which is a contradiction to
$z=0$
, which is a contradiction to
![]() $z\neq 0$
.
$z\neq 0$
.
Let
![]() $x\in V_{1}PV_{2}P^{1-t}\mathcal {M}\subset \mathcal {L}$
with
$x\in V_{1}PV_{2}P^{1-t}\mathcal {M}\subset \mathcal {L}$
with
![]() $x\neq 0$
. Then there exists a nonzero vector
$x\neq 0$
. Then there exists a nonzero vector
![]() $z\in \mathcal {M}$
such that
$z\in \mathcal {M}$
such that
![]() $ x=V_{1}PV_{2}P^{1-t}z$
. Note that
$ x=V_{1}PV_{2}P^{1-t}z$
. Note that
 $$ \begin{align*} \begin{array}{l} \left( T_{1}-\lambda T_{2}\right) x=T_{1}x-\lambda T_{2}x \\ =V_{1}P\left( V_{1}PV_{2}P^{1-t}z\right) -\lambda V_{2}P\left( V_{1}PV_{2}P^{1-t}z\right) \\ \overset{V_{1}PV_{2}=V_{2}PV_{1}}{=}V_{1}P\left( V_{2}PV_{1}P^{1-t}z\right) -\lambda V_{1}PV_{2}PV_{2}P^{1-t}z \\ =V_{1}PV_{2}P^{1-t}(\widehat{T_{1}^{t}}z)-\lambda V_{1}PV_{2}P^{1-t}( \widehat{T_{2}^{t}}z) \\ \in V_{1}PV_{2}P^{1-t}\mathcal{M}-\lambda V_{1}PV_{2}P^{1-t}\mathcal{M} \\ \subset \overline{V_{1}PV_{2}P^{1-t}\mathcal{M}}=\mathcal{L}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \left( T_{1}-\lambda T_{2}\right) x=T_{1}x-\lambda T_{2}x \\ =V_{1}P\left( V_{1}PV_{2}P^{1-t}z\right) -\lambda V_{2}P\left( V_{1}PV_{2}P^{1-t}z\right) \\ \overset{V_{1}PV_{2}=V_{2}PV_{1}}{=}V_{1}P\left( V_{2}PV_{1}P^{1-t}z\right) -\lambda V_{1}PV_{2}PV_{2}P^{1-t}z \\ =V_{1}PV_{2}P^{1-t}(\widehat{T_{1}^{t}}z)-\lambda V_{1}PV_{2}P^{1-t}( \widehat{T_{2}^{t}}z) \\ \in V_{1}PV_{2}P^{1-t}\mathcal{M}-\lambda V_{1}PV_{2}P^{1-t}\mathcal{M} \\ \subset \overline{V_{1}PV_{2}P^{1-t}\mathcal{M}}=\mathcal{L}. \end{array} \end{align*} $$
Thus,
![]() $\left ( T_{1}-\lambda T_{2}\right ) \mathcal {L\subset L}$
for all
$\left ( T_{1}-\lambda T_{2}\right ) \mathcal {L\subset L}$
for all
![]() $ \lambda \in \mathbb {C}$
and we have the desired one. Therefore, our proof is now completed.
$ \lambda \in \mathbb {C}$
and we have the desired one. Therefore, our proof is now completed.
As a corollary of Proposition 1.3 and Theorem 1.8, we obtain new proofs of the following results in [Reference Djordjević, Kim and Yoon8, Theorem 2.6] and [Reference Kim and Yoon13, Theorem 2.24].
Theorem 1.9 ([Reference Djordjević, Kim and Yoon8, Theorem 2.6], [Reference Kim and Yoon13, Theorem 2.24])
Let
![]() $ \mathbf {T}=(T_{1},T_{2})$
be a commuting pair of operators with dense ranges. Then, for
$ \mathbf {T}=(T_{1},T_{2})$
be a commuting pair of operators with dense ranges. Then, for
![]() $0\leq t\leq 1$
,
$0\leq t\leq 1$
,
![]() $\widehat {\mathbf {T}^{t}}$
has an NJIS if and only if
$\widehat {\mathbf {T}^{t}}$
has an NJIS if and only if
![]() $\mathbf {T}$
does.
$\mathbf {T}$
does.
Proof
![]() $\left ( \Longrightarrow \right ) $
For
$\left ( \Longrightarrow \right ) $
For
![]() $t=0$
, the desired one is clear.
$t=0$
, the desired one is clear.
For
![]() $0<t\leq 1$
, we assume that
$0<t\leq 1$
, we assume that
![]() $\widehat {\mathbf {T}^{t}}$
has an NJIS. Let
$\widehat {\mathbf {T}^{t}}$
has an NJIS. Let
![]() $\mathcal {M}\in \mathrm {Lat}\widehat {T_{1}^{t}}\cap \mathrm {Lat}\widehat { T_{2}^{t}}$
with
$\mathcal {M}\in \mathrm {Lat}\widehat {T_{1}^{t}}\cap \mathrm {Lat}\widehat { T_{2}^{t}}$
with
![]() $\mathcal {M}\neq \left \{ 0\right \} ,\mathcal {H}$
. Then, by Proposition 1.3, we have that
$\mathcal {M}\neq \left \{ 0\right \} ,\mathcal {H}$
. Then, by Proposition 1.3, we have that
![]() $\mathcal {M}\in \mathrm {Lat}\{ \widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
. Thus, by the proof of Theorem 1.8, we have that
$\mathcal {M}\in \mathrm {Lat}\{ \widehat {T_{1}^{t}}-\lambda \widehat {T_{2}^{t}}:\lambda \in \mathbb {C\}}$
. Thus, by the proof of Theorem 1.8, we have that
![]() $\mathcal {L}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, where
$\mathcal {L}\in \mathrm {Lat}\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C}\right \} $
, where
![]() $\mathcal {L}=\overline {V_{1}PV_{2}P^{1-t}\mathcal {M}}$
. By Proposition 1.3 again, we have that
$\mathcal {L}=\overline {V_{1}PV_{2}P^{1-t}\mathcal {M}}$
. By Proposition 1.3 again, we have that
![]() $\mathcal {L}\in \mathrm {Lat} T_{1}\cap \mathrm {Lat}T_{2}$
. Therefore,
$\mathcal {L}\in \mathrm {Lat} T_{1}\cap \mathrm {Lat}T_{2}$
. Therefore,
![]() $\mathbf {T}$
has an NIS, as desired.
$\mathbf {T}$
has an NIS, as desired.
![]() $\left ( \Longleftarrow \right ) $
It is clear from Proposition 1.3, Theorem 1.8, and the same argument given above.
$\left ( \Longleftarrow \right ) $
It is clear from Proposition 1.3, Theorem 1.8, and the same argument given above.
Next, we recall the following open problem.
Conjecture 1.10 [Reference Kim and Yoon13, Conjecture 2.29]
For a commuting n-tuple
![]() $ \mathbf {T}$
, we have that
$ \mathbf {T}$
, we have that
![]() $\mathrm {Lat}\left ( \mathbf {T}\right ) $
and
$\mathrm {Lat}\left ( \mathbf {T}\right ) $
and
![]() $ \mathrm {Lat}(\widehat {\mathbf {T}^{t}}) \left ( t=1\right ) $
are isomorphic.
$ \mathrm {Lat}(\widehat {\mathbf {T}^{t}}) \left ( t=1\right ) $
are isomorphic.
The following result gives a partial answer to Conjecture 1.10 and more.
Example 1.11 Let R and Q be positive operators in
![]() $\mathcal {B(H)}$
such that
$\mathcal {B(H)}$
such that
![]() $\left [ R,Q\right ] =RQ-QR\neq 0$
and
$\left [ R,Q\right ] =RQ-QR\neq 0$
and
![]() $R+Q$
is invertible. Consider the linear pencil
$R+Q$
is invertible. Consider the linear pencil
![]() $\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C} \right \} $
, where
$\left \{ T_{1}-\lambda T_{2}:\lambda \in \mathbb {C} \right \} $
, where
![]() $(T_{1},T_{2})=(\sqrt {R},\sqrt {Q})$
. Then we have that for
$(T_{1},T_{2})=(\sqrt {R},\sqrt {Q})$
. Then we have that for
![]() $0\leq t\leq 1$
,
$0\leq t\leq 1$
,
![]() $\mathrm {Lat}(\widehat {\mathbf {T}^{t}})=\mathrm {Lat} \left ( \mathbf {T}\right ) $
. For this, note that
$\mathrm {Lat}(\widehat {\mathbf {T}^{t}})=\mathrm {Lat} \left ( \mathbf {T}\right ) $
. For this, note that
![]() $T_{1}^{\ast }T_{1}+T_{2}^{\ast }T_{2}=R+Q$
and
$T_{1}^{\ast }T_{1}+T_{2}^{\ast }T_{2}=R+Q$
and
![]() $P=\sqrt {R+Q}$
is invertible. Thus, the polar decomposition of the pencil is
$P=\sqrt {R+Q}$
is invertible. Thus, the polar decomposition of the pencil is
because for
![]() $i=1,2$
,
$i=1,2$
,
![]() $V_{i}=T_{i}P^{-1}$
. So, the generalized Aluthge transform is
$V_{i}=T_{i}P^{-1}$
. So, the generalized Aluthge transform is
Hence, by Proposition 1.3, we have that for
![]() $0\leq t\leq 1$
,
$0\leq t\leq 1$
,
 $$ \begin{align*} \mathrm{Lat}(\widehat{\mathbf{T}^{t}}) &= \mathrm{Lat}\widehat{T_{1}^{t}} \cap \mathrm{Lat}\widehat{T_{2}^{t}}=\mathrm{Lat}\{\widehat{T_{1}^{t}} -\lambda \widehat{T_{2}^{t}}:\lambda \in \mathbb{C}\} \\ &=\mathrm{Lat}\left\{ P^{t}T_{1}P^{-t}-\lambda P^{t}T_{2}P^{-t}:\lambda \in \mathbb{C}\right\} \\ &=\mathrm{Lat}(P^{t}T_{1}P^{-t})\cap \mathrm{Lat}(P^{t}T_{2}P^{-t}) \\ &=\mathrm{Lat}T_{1}\cap \mathrm{Lat}T_{2}=\mathrm{Lat}\left( \mathbf{T} \right){\kern-2pt}. \end{align*} $$
$$ \begin{align*} \mathrm{Lat}(\widehat{\mathbf{T}^{t}}) &= \mathrm{Lat}\widehat{T_{1}^{t}} \cap \mathrm{Lat}\widehat{T_{2}^{t}}=\mathrm{Lat}\{\widehat{T_{1}^{t}} -\lambda \widehat{T_{2}^{t}}:\lambda \in \mathbb{C}\} \\ &=\mathrm{Lat}\left\{ P^{t}T_{1}P^{-t}-\lambda P^{t}T_{2}P^{-t}:\lambda \in \mathbb{C}\right\} \\ &=\mathrm{Lat}(P^{t}T_{1}P^{-t})\cap \mathrm{Lat}(P^{t}T_{2}P^{-t}) \\ &=\mathrm{Lat}T_{1}\cap \mathrm{Lat}T_{2}=\mathrm{Lat}\left( \mathbf{T} \right){\kern-2pt}. \end{align*} $$