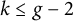1 Introduction
Let X be a smooth projective curve of genus g over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $\operatorname {Jac}(X)$
be its Jacobian. Let
$\operatorname {Jac}(X)$
be its Jacobian. Let
![]() $\operatorname {CH}_k(\operatorname {Jac}(X))_{\hom }$
be the Chow group of homologically trivial algebraic cycles of dimension k on
$\operatorname {CH}_k(\operatorname {Jac}(X))_{\hom }$
be the Chow group of homologically trivial algebraic cycles of dimension k on
![]() $\operatorname {Jac}(X)$
modulo rational equivalence. To study this group, we consider the Abel-Jacobi map
$\operatorname {Jac}(X)$
modulo rational equivalence. To study this group, we consider the Abel-Jacobi map
Here,
![]() $J_k(\operatorname {Jac}(X))$
is a complex torus, which is called the Griffiths intermediate Jacobian (see Section 3.1). It is well known that
$J_k(\operatorname {Jac}(X))$
is a complex torus, which is called the Griffiths intermediate Jacobian (see Section 3.1). It is well known that
![]() $\Phi _{g-1}$
is an isomorphism by the Abel-Jacobi theorem; however, for a general k,
$\Phi _{g-1}$
is an isomorphism by the Abel-Jacobi theorem; however, for a general k,
![]() $\Phi _k$
is neither injective nor surjective. Fix a base point
$\Phi _k$
is neither injective nor surjective. Fix a base point
![]() $e \in X$
and let
$e \in X$
and let
![]() $\iota _e$
be the embedding defined by
$\iota _e$
be the embedding defined by
Put
![]() $X_e=\iota _e(X)$
. We denote
$X_e=\iota _e(X)$
. We denote
![]() $X_e^-$
by the image of
$X_e^-$
by the image of
![]() $X_e$
under the inversion map. Since the inversion map acts trivially on the cohomology groups of even degree, we have
$X_e$
under the inversion map. Since the inversion map acts trivially on the cohomology groups of even degree, we have
Let
![]() $W_{k, e}$
be the image of the k-th symmetric product of X on
$W_{k, e}$
be the image of the k-th symmetric product of X on
![]() $\operatorname {Jac}(X)$
. As in the case of
$\operatorname {Jac}(X)$
. As in the case of
![]() $k=1$
, we have
$k=1$
, we have
These cycles are called the Ceresa cycles and for a generic curve X, Ceresa [Reference Ceresa4] proves that if
![]() $1 \leq k \leq g-2$
, then
$1 \leq k \leq g-2$
, then
![]() $W_{k,e} - W_{k,e}^-$
is nontrivial modulo algebraic equivalence.
$W_{k,e} - W_{k,e}^-$
is nontrivial modulo algebraic equivalence.
For a positive integer N and integers
![]() $a, b \in \{1, \ldots , N-1\}$
, let
$a, b \in \{1, \ldots , N-1\}$
, let
![]() $C_N^{a, b}$
be the smooth projective curve birational to the affine curve
$C_N^{a, b}$
be the smooth projective curve birational to the affine curve
Let
![]() $F_N$
be the Fermat curve of degree N. Then
$F_N$
be the Fermat curve of degree N. Then
![]() $C_N^{a, b}$
is a quotient of
$C_N^{a, b}$
is a quotient of
![]() $F_N$
by a cyclic group
$F_N$
by a cyclic group
![]() $G_N^{a, b}$
(see Section 2). Let g be the genus of
$G_N^{a, b}$
(see Section 2). Let g be the genus of
![]() $C_N^{a, b}$
. The main theorem of this paper is as follows.
$C_N^{a, b}$
. The main theorem of this paper is as follows.
Theorem 1.1 Suppose that N has a prime divisor
![]() $p>7$
such that
$p>7$
such that
![]() $p \nmid ab$
and
$p \nmid ab$
and
![]() $a^2+ab+b^2 \equiv 0 \ \ \pmod {p}$
. Then
$a^2+ab+b^2 \equiv 0 \ \ \pmod {p}$
. Then
![]() $\Phi _k(W_{k, e}-W_{k, e}^-) \in J_k(\operatorname {Jac}(C_N^{a, b}))$
is non-torsion for any choice of the base point
$\Phi _k(W_{k, e}-W_{k, e}^-) \in J_k(\operatorname {Jac}(C_N^{a, b}))$
is non-torsion for any choice of the base point
![]() $e \in C_N^{a, b}$
and
$e \in C_N^{a, b}$
and
![]() $k=1, \ldots , g-2$
.
$k=1, \ldots , g-2$
.
Remark 1.2 When N does not have a prime divisor
![]() $p>7$
, there exist some examples that the Abel-Jacobi image of the Ceresa cycle of
$p>7$
, there exist some examples that the Abel-Jacobi image of the Ceresa cycle of
![]() $C_N^{a, b}$
is torsion. For example,
$C_N^{a, b}$
is torsion. For example,
![]() ${\Phi _1(X_e-X_e^-)}$
is torsion for
${\Phi _1(X_e-X_e^-)}$
is torsion for
![]() $X=C_{9}^{1, 2}$
,
$X=C_{9}^{1, 2}$
,
![]() $C_{12}^{1, 3}$
,
$C_{12}^{1, 3}$
,
![]() $C_{15}^{1, 5}$
and
$C_{15}^{1, 5}$
and
![]() $e=(0, 0)$
([Reference Beauville1, §2 Theorem], [Reference Lilienfeldt and Shnidman15, Theorem 3.2]).
$e=(0, 0)$
([Reference Beauville1, §2 Theorem], [Reference Lilienfeldt and Shnidman15, Theorem 3.2]).
The algebraical nontriviality of the Ceresa cycles of
![]() $F_N$
(
$F_N$
(
![]() $N \leq 1000$
) and
$N \leq 1000$
) and
![]() $C_p^{1, b}$
(
$C_p^{1, b}$
(
![]() ${p \leq 1000}$
is a prime and
${p \leq 1000}$
is a prime and
![]() $b^2+b+1 \equiv 0 \ \ \pmod {p}$
) is proved by Harris [Reference Harris10], Bloch [Reference Bloch2], Kimura [Reference Kimura14], Tadokoro [Reference Tadokoro18, Reference Tadokoro19, Reference Tadokoro20], and Otsubo [Reference Otsubo16]. Moreover, Otsubo [Reference Otsubo16] and Tadokoro [Reference Tadokoro20] give a sufficient condition for the Ceresa cycles of these to be non-torsion modulo algebraic equivalence; however, it is impossible to confirm numerically these conditions. There are only two explicit examples of non-torsioness modulo algebraic equivalence for
$b^2+b+1 \equiv 0 \ \ \pmod {p}$
) is proved by Harris [Reference Harris10], Bloch [Reference Bloch2], Kimura [Reference Kimura14], Tadokoro [Reference Tadokoro18, Reference Tadokoro19, Reference Tadokoro20], and Otsubo [Reference Otsubo16]. Moreover, Otsubo [Reference Otsubo16] and Tadokoro [Reference Tadokoro20] give a sufficient condition for the Ceresa cycles of these to be non-torsion modulo algebraic equivalence; however, it is impossible to confirm numerically these conditions. There are only two explicit examples of non-torsioness modulo algebraic equivalence for
![]() $k=1$
:
$k=1$
:
![]() $F_4$
by Bloch [Reference Bloch2] and
$F_4$
by Bloch [Reference Bloch2] and
![]() $C_7^{1, 2}$
by Kimura [Reference Kimura14]; they prove the non-torsioness of the l-adic Abel-Jacobi image.
$C_7^{1, 2}$
by Kimura [Reference Kimura14]; they prove the non-torsioness of the l-adic Abel-Jacobi image.
Let N be a positive integer divisible by a prime
![]() $p> 7$
. Eskandari-Murty [Reference Eskandari and Murty6, Reference Eskandari and Murty7] prove that
$p> 7$
. Eskandari-Murty [Reference Eskandari and Murty6, Reference Eskandari and Murty7] prove that
![]() $\Phi _1(F_{N, e} -F_{N, e}^-)$
is non-torsion for any
$\Phi _1(F_{N, e} -F_{N, e}^-)$
is non-torsion for any
![]() $e \in F_N$
; in particular,
$e \in F_N$
; in particular,
![]() $F_{N, e} -F_{N, e}^-$
is non-torsion modulo rational equivalence. Moreover, they conjecture that the same result holds for
$F_{N, e} -F_{N, e}^-$
is non-torsion modulo rational equivalence. Moreover, they conjecture that the same result holds for
![]() $C_p^{1, m}$
with
$C_p^{1, m}$
with
![]() $m \in \{1, \ldots , p-2\}$
and
$m \in \{1, \ldots , p-2\}$
and
![]() $m \neq 1, (p-1)/2, p-2$
[Reference Eskandari and Murty7, Section 4, Remark (2)]. Theorem 1.1 partially but affirmatively answers their conjecture.
$m \neq 1, (p-1)/2, p-2$
[Reference Eskandari and Murty7, Section 4, Remark (2)]. Theorem 1.1 partially but affirmatively answers their conjecture.
We briefly give a sketch of the proof. First, we reduce to the case
![]() $k=1$
using a method of Otsubo [Reference Otsubo16] (see Proposition 3.1). The reduction to the case
$k=1$
using a method of Otsubo [Reference Otsubo16] (see Proposition 3.1). The reduction to the case
![]() $N=p$
is easy. The rest of the proof is parallel to the method of Eskandari-Murty [Reference Eskandari and Murty6, Reference Eskandari and Murty7]. First, the Abel-Jacobi image of the Ceresa cycle is described by an extension of mixed Hodge structures by Harris [Reference Harris10] and Pulte [Reference Pulte17] (see Section 3.2). Second, we construct a
$N=p$
is easy. The rest of the proof is parallel to the method of Eskandari-Murty [Reference Eskandari and Murty6, Reference Eskandari and Murty7]. First, the Abel-Jacobi image of the Ceresa cycle is described by an extension of mixed Hodge structures by Harris [Reference Harris10] and Pulte [Reference Pulte17] (see Section 3.2). Second, we construct a
![]() $1$
-cycle Z on
$1$
-cycle Z on
![]() $C_p^{a,b} \times C_p^{a,b}$
and evaluate the extension of mixed Hodge structures at Z. Here, we use the assumptions on a and b so that an automorphism of
$C_p^{a,b} \times C_p^{a,b}$
and evaluate the extension of mixed Hodge structures at Z. Here, we use the assumptions on a and b so that an automorphism of
![]() $F_p$
of order
$F_p$
of order
![]() $3$
descends to
$3$
descends to
![]() $C_p^{a, b}$
. Then the extension class is expressed by a rational point
$C_p^{a, b}$
. Then the extension class is expressed by a rational point
![]() $P_Z \in \operatorname {Jac}(C_N^{a, b})$
by formulas of Kaenders [Reference Kaenders13] and Darmon-Rotger-Sols [Reference Darmon, Rotger and Sols5] (see Sections 3.3, 3.4). Finally, since
$P_Z \in \operatorname {Jac}(C_N^{a, b})$
by formulas of Kaenders [Reference Kaenders13] and Darmon-Rotger-Sols [Reference Darmon, Rotger and Sols5] (see Sections 3.3, 3.4). Finally, since
![]() $P_Z$
is non-torsion by a result of Gross-Rohrlich [Reference Gross and Rohrlich8] (see Section 2), where we use the assumption
$P_Z$
is non-torsion by a result of Gross-Rohrlich [Reference Gross and Rohrlich8] (see Section 2), where we use the assumption
![]() $p> 7$
, the theorem follows.
$p> 7$
, the theorem follows.
2 Fermat quotient curves
Let
![]() $N>3$
be an integer, and for integers
$N>3$
be an integer, and for integers
![]() $a, b\in \{1, \ldots , N-1\}$
, let
$a, b\in \{1, \ldots , N-1\}$
, let
![]() $C^{a, b}_N$
be the smooth projective curve birational to
$C^{a, b}_N$
be the smooth projective curve birational to
The map
is ramified at
![]() $x=0, 1$
and
$x=0, 1$
and
![]() $\infty $
. Above
$\infty $
. Above
![]() $0$
(resp.
$0$
(resp.
![]() $1$
,
$1$
,
![]() $\infty $
), there are
$\infty $
), there are
![]() $\gcd (N, a)$
(resp.
$\gcd (N, a)$
(resp.
![]() $\gcd (N, b)$
,
$\gcd (N, b)$
,
![]() $\gcd (N, a+b)$
) branches and the ramification index is
$\gcd (N, a+b)$
) branches and the ramification index is
![]() $N/\gcd (N, a)$
(resp.
$N/\gcd (N, a)$
(resp.
![]() $N/\gcd (N, b)$
,
$N/\gcd (N, b)$
,
![]() $N/\gcd (N, a+b)$
). Therefore, by the Riemann-Hurwitz formula, the genus of
$N/\gcd (N, a+b)$
). Therefore, by the Riemann-Hurwitz formula, the genus of
![]() $C^{a, b}_N$
is
$C^{a, b}_N$
is
We have an isomorphism
sending x to
![]() $1-x$
. If two other integers
$1-x$
. If two other integers
![]() $a', b' \in \{1, \ldots , N-1\}$
satisfy the relation
$a', b' \in \{1, \ldots , N-1\}$
satisfy the relation
for some integers
![]() $h, i, j$
with
$h, i, j$
with
![]() $\gcd (N, h)=1$
, we have
$\gcd (N, h)=1$
, we have
Let
![]() $F_N$
be the Fermat curve of degree N defined by
$F_N$
be the Fermat curve of degree N defined by
Then there is a morphism
Define a finite group by
and denote an element
![]() $(r, s) \in G_N$
by
$(r, s) \in G_N$
by
![]() $g_N^{r, s}$
. Fix a primitive N-th root of unity
$g_N^{r, s}$
. Fix a primitive N-th root of unity
![]() $\zeta _N$
and let
$\zeta _N$
and let
![]() $G_N$
act on
$G_N$
act on
![]() $F_N$
by
$F_N$
by
Let
![]() $G_N^{a, b}$
be a subgroup of
$G_N^{a, b}$
be a subgroup of
![]() $G_N$
defined by
$G_N$
defined by
If
![]() $\gcd (N, a, b)=1$
,
$\gcd (N, a, b)=1$
,
![]() $F_N$
is generically Galois over
$F_N$
is generically Galois over
![]() $C^{a, b}_N$
and
$C^{a, b}_N$
and
There is an automorphism
![]() $\alpha $
of
$\alpha $
of
![]() $F_N$
of order
$F_N$
of order
![]() $2$
defined by
$2$
defined by
When N is odd, there is an automorphism
![]() $\beta $
of
$\beta $
of
![]() $F_N$
of order
$F_N$
of order
![]() $3$
defined by
$3$
defined by
Lemma 2.1 (cf. [Reference Irokawa and Sasaki12, Section 3.1])
Suppose that
![]() $\gcd (N, a, b)=1$
. Then,
$\gcd (N, a, b)=1$
. Then,
-
(i)
 $\alpha $
descends to
$\alpha $
descends to
 $C^{a, b}_N$
if and only if
$C^{a, b}_N$
if and only if
 $a^2 \equiv b^2 \ \ \pmod {N}$
.
$a^2 \equiv b^2 \ \ \pmod {N}$
. -
(ii) Suppose that N is odd. Then
 $\beta $
descends to
$\beta $
descends to
 $C^{a, b}_N$
if and only if
$C^{a, b}_N$
if and only if
 $a^2+ab+b^2 \equiv 0 \ \ \pmod {N}$
. We denote this automorphism by
$a^2+ab+b^2 \equiv 0 \ \ \pmod {N}$
. We denote this automorphism by
 $\widetilde {\beta }$
.
$\widetilde {\beta }$
.
Proof We only prove (ii) since we use the morphism
![]() $\widetilde {\beta }$
to prove Theorem 1.1 and (i) is similarly proved. The automorphism
$\widetilde {\beta }$
to prove Theorem 1.1 and (i) is similarly proved. The automorphism
![]() $\beta $
descends to
$\beta $
descends to
![]() $\widetilde {\beta }$
if and only if
$\widetilde {\beta }$
if and only if
that is, there exists an integer i such that
for all
![]() $(u : v: w) \in F_N$
. This is equivalent to
$(u : v: w) \in F_N$
. This is equivalent to
First, (2.1) implies
![]() $a^2+ab+b^2 \kern1.3pt{\equiv}\kern1.3pt 0 \,\ \pmod {N}$
. However, if
$a^2+ab+b^2 \kern1.3pt{\equiv}\kern1.3pt 0 \,\ \pmod {N}$
. However, if
![]() $a^2+ab+b^2 \kern1.3pt{\equiv}\kern1.3pt 0 \,\ \pmod {N}$
, then we have
$a^2+ab+b^2 \kern1.3pt{\equiv}\kern1.3pt 0 \,\ \pmod {N}$
, then we have
![]() $\gcd (N,a)=\gcd (N, b)=1$
by the assumption
$\gcd (N,a)=\gcd (N, b)=1$
by the assumption
![]() $\gcd (N, a, b)=1$
. Therefore, there is an integer i such that
$\gcd (N, a, b)=1$
. Therefore, there is an integer i such that
![]() $ai \equiv b \ \ \pmod {N}$
, which satisfies (2.1).
$ai \equiv b \ \ \pmod {N}$
, which satisfies (2.1).
Remark 2.2
-
(i) If N is a prime, the condition
 $a^2+ab+b^2 \equiv 0 \ \ \pmod {N}$
implies that
$a^2+ab+b^2 \equiv 0 \ \ \pmod {N}$
implies that
 $N \equiv 1 \ \ \pmod {3}$
.
$N \equiv 1 \ \ \pmod {3}$
. -
(ii) When
 $N=a^2+ab+b^2$
, the curve
$N=a^2+ab+b^2$
, the curve
 $C^{a, b}_N$
is isomorphic to the Hurwitz curve ([Reference Irokawa and Sasaki12, Lemma 3.8]) which is the smooth projective curve birational to
$C^{a, b}_N$
is isomorphic to the Hurwitz curve ([Reference Irokawa and Sasaki12, Lemma 3.8]) which is the smooth projective curve birational to  $$ \begin{align*}X^{b}Y^{a+b}+Y^{b}Z^{a+b}+Z^{b}X^{a+b}=0.\end{align*} $$
$$ \begin{align*}X^{b}Y^{a+b}+Y^{b}Z^{a+b}+Z^{b}X^{a+b}=0.\end{align*} $$
-
(iii) The condition
 $a^2+ab+b^2 \equiv 0 \ \ \pmod {N}$
(for N prime) appears in Tadokoro [Reference Tadokoro20]. He uses
$a^2+ab+b^2 \equiv 0 \ \ \pmod {N}$
(for N prime) appears in Tadokoro [Reference Tadokoro20]. He uses
 $\widetilde {\beta }$
to construct from a
$\widetilde {\beta }$
to construct from a
 $1$
-form
$1$
-form
 $\omega $
on
$\omega $
on
 $C_N^{a, b}$
two other
$C_N^{a, b}$
two other
 $1$
-forms of the same Hodge type and evaluate the Abel-Jacobi image of the Ceresa cycle for
$1$
-forms of the same Hodge type and evaluate the Abel-Jacobi image of the Ceresa cycle for
 $k=1$
at
$k=1$
at
 $\omega \wedge \widetilde {\beta }^* \omega \wedge (\widetilde {\beta }^2)^*\omega $
.
$\omega \wedge \widetilde {\beta }^* \omega \wedge (\widetilde {\beta }^2)^*\omega $
.
When
![]() $\gcd (N, 6)=1$
, the automorphism
$\gcd (N, 6)=1$
, the automorphism
![]() $\beta $
of
$\beta $
of
![]() $F_N$
has two fixed points
$F_N$
has two fixed points
and there is no other fixed point.
Lemma 2.3 Suppose that
![]() $\gcd (N, a, b)=\gcd (N, 6)=1$
and
$\gcd (N, a, b)=\gcd (N, 6)=1$
and
![]() $a^2+ab+b^2 \equiv 0 \pmod {N}$
. Then the fixed points of the automorphism
$a^2+ab+b^2 \equiv 0 \pmod {N}$
. Then the fixed points of the automorphism
![]() $\widetilde {\beta }$
of
$\widetilde {\beta }$
of
![]() $C^{a, b}_N$
are
$C^{a, b}_N$
are
![]() $\pi _N^{a, b}(S)$
and
$\pi _N^{a, b}(S)$
and
![]() $\pi _N^{a, b}(\overline {S})$
, which are distinct.
$\pi _N^{a, b}(\overline {S})$
, which are distinct.
Proof We regard a, b as elements in
![]() $(\mathbb {Z}/N\mathbb {Z})^*$
. Put
$(\mathbb {Z}/N\mathbb {Z})^*$
. Put
![]() $\gamma =g_N^{b, -a}$
. Then we have
$\gamma =g_N^{b, -a}$
. Then we have
since
![]() $-a-b=a^{-1}b^2$
by the assumption
$-a-b=a^{-1}b^2$
by the assumption
![]() $a^2+ab+b^2=0$
in
$a^2+ab+b^2=0$
in
![]() $\mathbb {Z}/N\mathbb {Z}$
. For
$\mathbb {Z}/N\mathbb {Z}$
. For
![]() $P \in C_N^{a, b}$
, suppose that
$P \in C_N^{a, b}$
, suppose that
![]() $\widetilde {\beta }(P)=P$
and take any
$\widetilde {\beta }(P)=P$
and take any
![]() $Q \in F_N$
such that
$Q \in F_N$
such that
![]() $\pi _N^{a, b}(Q)=P$
. Then
$\pi _N^{a, b}(Q)=P$
. Then
for some
![]() $k \in \mathbb {Z}/N\mathbb {Z}$
. Since
$k \in \mathbb {Z}/N\mathbb {Z}$
. Since
![]() $(a-b)^2=3ab \in (\mathbb {Z}/N\mathbb {Z})^*$
, we have
$(a-b)^2=3ab \in (\mathbb {Z}/N\mathbb {Z})^*$
, we have
![]() $a-b \in (\mathbb {Z}/N\mathbb {Z})^*$
. We take
$a-b \in (\mathbb {Z}/N\mathbb {Z})^*$
. We take
![]() $i=a(a-b)^{-1}k$
. Then we have
$i=a(a-b)^{-1}k$
. Then we have
which means that
![]() $\gamma ^i Q=S$
or
$\gamma ^i Q=S$
or
![]() $\overline {S}$
; hence,
$\overline {S}$
; hence,
![]() $P=\pi _N^{a, b}(S)$
or
$P=\pi _N^{a, b}(S)$
or
![]() $\pi _N^{a, b}(\overline {S})$
.
$\pi _N^{a, b}(\overline {S})$
.
We are to show that
![]() $\pi _N^{a, b}(S) \neq \pi _N^{a, b}(\overline {S})$
. Suppose that
$\pi _N^{a, b}(S) \neq \pi _N^{a, b}(\overline {S})$
. Suppose that
![]() $\pi _N^{a, b}(S) = \pi _N^{a, b}(\overline {S})$
; that is, there exists an integer i such that
$\pi _N^{a, b}(S) = \pi _N^{a, b}(\overline {S})$
; that is, there exists an integer i such that
Then we have
![]() $\zeta _6^{2N}=1$
, which contradicts the assumption
$\zeta _6^{2N}=1$
, which contradicts the assumption
![]() $\gcd (N, 6)=1$
.
$\gcd (N, 6)=1$
.
Put
![]() $P_0\kern1.3pt{=}\kern1.3pt(0 : 1: 1) \kern1.3pt{\in}\kern1.3pt F_N$
and let
$P_0\kern1.3pt{=}\kern1.3pt(0 : 1: 1) \kern1.3pt{\in}\kern1.3pt F_N$
and let
![]() $F_N \kern1.3pt{\to}\kern1.3pt \operatorname {Jac}(F_N)$
be the map defined by
$F_N \kern1.3pt{\to}\kern1.3pt \operatorname {Jac}(F_N)$
be the map defined by
![]() ${Q \kern1.3pt{\mapsto}\kern1.3pt [Q]-[P_0]}$
. Similarly, we define a map
${Q \kern1.3pt{\mapsto}\kern1.3pt [Q]-[P_0]}$
. Similarly, we define a map
![]() $C^{a, b}_N \to \operatorname {Jac}(C^{a, b}_N)$
by sending
$C^{a, b}_N \to \operatorname {Jac}(C^{a, b}_N)$
by sending
![]() $Q'$
to
$Q'$
to
![]() $[Q'] - [\pi _N^{a, b}(P_0)]$
. Then we have a commutative diagram
$[Q'] - [\pi _N^{a, b}(P_0)]$
. Then we have a commutative diagram

The following result of Gross and Rohrlich is one of the key ingredients to the proof of Theorem 1.1.
Theorem 2.4 [Reference Gross and Rohrlich8, Theorem 2.1]
Let N be an integer such that
![]() $\gcd (N, 6)=1$
and N is divisible by a prime
$\gcd (N, 6)=1$
and N is divisible by a prime
![]() $p>7$
. If
$p>7$
. If
![]() $a-b, a+2b, 2a+b \not \equiv 0 \ \ \pmod {p}$
, then the point
$a-b, a+2b, 2a+b \not \equiv 0 \ \ \pmod {p}$
, then the point
![]() $(\pi _N^{a, b})_*([S]+[\overline {S}] -2[P_0])$
on
$(\pi _N^{a, b})_*([S]+[\overline {S}] -2[P_0])$
on
![]() $\operatorname {Jac}(C^{a, b}_N)$
is non-torsion.
$\operatorname {Jac}(C^{a, b}_N)$
is non-torsion.
3 Algebraic cycles and Hodge theory of quadratic iterated integrals
3.1 Extension of mixed Hodge structures
Let
![]() $R=\mathbb {Z}$
or
$R=\mathbb {Z}$
or
![]() $\mathbb {Q}$
. An R-mixed Hodge structure H is an R-module
$\mathbb {Q}$
. An R-mixed Hodge structure H is an R-module
![]() $H_R$
of finite rank equipped with an increasing weight filtration
$H_R$
of finite rank equipped with an increasing weight filtration
![]() $W_{\bullet }$
on
$W_{\bullet }$
on
![]() $H_{\mathbb {Q}}:=H_R \otimes _{R} \mathbb {Q}$
and a decreasing Hodge filtration
$H_{\mathbb {Q}}:=H_R \otimes _{R} \mathbb {Q}$
and a decreasing Hodge filtration
![]() $F^{\bullet }$
on
$F^{\bullet }$
on
![]() $H_{\mathbb {C}}:=H_R \otimes _{R} \mathbb {C}$
such that for each k,
$H_{\mathbb {C}}:=H_R \otimes _{R} \mathbb {C}$
such that for each k,
![]() $\mathrm {Gr}_k^W(H_{\mathbb {Q}})$
with the induced filtration
$\mathrm {Gr}_k^W(H_{\mathbb {Q}})$
with the induced filtration
![]() $F^{\bullet }$
is a pure
$F^{\bullet }$
is a pure
![]() $\mathbb {Q}$
-Hodge structure of weight k. Let
$\mathbb {Q}$
-Hodge structure of weight k. Let
![]() $R(n)$
be the Tate object of pure weight
$R(n)$
be the Tate object of pure weight
![]() $-2n$
and put
$-2n$
and put
![]() $H(n)=H\otimes _{R} R(n)$
. Let
$H(n)=H\otimes _{R} R(n)$
. Let
![]() $H^{\vee }$
be the dual R-mixed Hodge structure of H.
$H^{\vee }$
be the dual R-mixed Hodge structure of H.
Let MHS
![]() $(R)$
be the category of R-mixed Hodge structures. For R-mixed Hodge structures A, B, let
$(R)$
be the category of R-mixed Hodge structures. For R-mixed Hodge structures A, B, let
![]() $\mathrm {Ext}_{\mathrm {MHS}(R)}(A, B)$
denote the set of equivalence classes of extensions of R-mixed Hodge structures (i.e., exact sequences
$\mathrm {Ext}_{\mathrm {MHS}(R)}(A, B)$
denote the set of equivalence classes of extensions of R-mixed Hodge structures (i.e., exact sequences
of R-mixed Hodge structures up to natural equivalence relation). There is a natural operation called the Baer sum which makes
![]() $\mathrm {Ext}_{\mathrm {MHS}(R)}(A, B)$
an abelian group. If X is a smooth projective variety over
$\mathrm {Ext}_{\mathrm {MHS}(R)}(A, B)$
an abelian group. If X is a smooth projective variety over
![]() $\mathbb {C}$
, the cohomology group
$\mathbb {C}$
, the cohomology group
![]() $H^n(X, \mathbb {Z})$
underlies a pure
$H^n(X, \mathbb {Z})$
underlies a pure
![]() $\mathbb {Z}$
-Hodge structure of weight n, which we denote by
$\mathbb {Z}$
-Hodge structure of weight n, which we denote by
![]() $H^n(X)$
.
$H^n(X)$
.
For a pure
![]() $\mathbb {Z}$
-Hodge structure H of weight
$\mathbb {Z}$
-Hodge structure H of weight
![]() $-1$
, the intermediate Jacobian is defined by
$-1$
, the intermediate Jacobian is defined by
which is a complex torus. We have Carlson’s isomorphism [Reference Carlson3]
For a smooth projective variety X over
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $H_{2k+1}(X)(-k)$
is a pure
$H_{2k+1}(X)(-k)$
is a pure
![]() $\mathbb {Z}$
-Hodge structure of weight
$\mathbb {Z}$
-Hodge structure of weight
![]() $-1$
, and
$-1$
, and
is the k-th intermediate Jacobian of Griffiths. The Carlson isomorphism is written as
Let
![]() $\operatorname {CH}_k(X)$
be the Chow group of k-dimensional algebraic cycles on X modulo rational equivalence, and
$\operatorname {CH}_k(X)$
be the Chow group of k-dimensional algebraic cycles on X modulo rational equivalence, and
![]() $\operatorname {CH}_k(X)_{\mathrm {hom}}$
be the subgroup of homologically trivial cycles. Then we have the Abel-Jacobi map
$\operatorname {CH}_k(X)_{\mathrm {hom}}$
be the subgroup of homologically trivial cycles. Then we have the Abel-Jacobi map
for any
![]() $\eta \in F^{k+1}H^{2k+1}(X, \mathbb {C})$
, where
$\eta \in F^{k+1}H^{2k+1}(X, \mathbb {C})$
, where
![]() $\Gamma $
is a topological
$\Gamma $
is a topological
![]() $(2k+1)$
-chain such that
$(2k+1)$
-chain such that
![]() ${\partial \Gamma = Z}$
.
${\partial \Gamma = Z}$
.
From now on, let X be a smooth projective curve of genus
![]() $g \geq 3$
over
$g \geq 3$
over
![]() $\mathbb {C}$
. Let
$\mathbb {C}$
. Let
be the cup product
![]() $\varphi \otimes \varphi ' \mapsto \int _X \varphi \wedge \varphi '$
. Choosing a base point
$\varphi \otimes \varphi ' \mapsto \int _X \varphi \wedge \varphi '$
. Choosing a base point
![]() $e \in X$
, X is embedded into
$e \in X$
, X is embedded into
![]() $\operatorname {Jac}(X)$
sending e to zero. It induces isomorphisms
$\operatorname {Jac}(X)$
sending e to zero. It induces isomorphisms
which do not depend on the choice of e. We identify these and denote them by
![]() $H_1$
and
$H_1$
and
![]() $H^1$
, respectively. Recall that the cup product induces an isomorphism
$H^1$
, respectively. Recall that the cup product induces an isomorphism
For
![]() $e \in X$
, let
$e \in X$
, let
![]() $\iota _e \colon X \to \operatorname {Jac}(X)$
be the map defined by
$\iota _e \colon X \to \operatorname {Jac}(X)$
be the map defined by
![]() $P \mapsto [P]-[e]$
. Let
$P \mapsto [P]-[e]$
. Let
![]() $X^k$
(resp.
$X^k$
(resp.
![]() $\operatorname {Jac}(X)^k$
) be the k-fold product of X (resp.
$\operatorname {Jac}(X)^k$
) be the k-fold product of X (resp.
![]() $\operatorname {Jac}(X)$
) and
$\operatorname {Jac}(X)$
) and
![]() $\mu \colon \operatorname {Jac}(X)^k \to \operatorname {Jac}(X)$
be the addition. We put
$\mu \colon \operatorname {Jac}(X)^k \to \operatorname {Jac}(X)$
be the addition. We put
Then
![]() $W_{k, e}$
defines an algebraic k-cycle on
$W_{k, e}$
defines an algebraic k-cycle on
![]() $\operatorname {Jac}(X)$
, and
$\operatorname {Jac}(X)$
, and
![]() $W_{k, e}-W_{k, e}^-$
defines an element of
$W_{k, e}-W_{k, e}^-$
defines an element of
![]() $\operatorname {CH}_k(\operatorname {Jac}(X))_{\mathrm {hom}}$
.
$\operatorname {CH}_k(\operatorname {Jac}(X))_{\mathrm {hom}}$
.
Proposition 3.1 If
![]() $\Phi _1(X_e -X_e^-)$
is non-torsion, then
$\Phi _1(X_e -X_e^-)$
is non-torsion, then
![]() $\Phi _k(W_{k, e}-W_{k, e}^-)$
is non-torsion for any
$\Phi _k(W_{k, e}-W_{k, e}^-)$
is non-torsion for any
![]() $k=2, \ldots , g-2$
.
$k=2, \ldots , g-2$
.
Proof Let
![]() $S=\{e_i, f_i \mid 1 \leq i \leq g\}$
be a symplectic basis of
$S=\{e_i, f_i \mid 1 \leq i \leq g\}$
be a symplectic basis of
![]() $H^1_{\mathbb {Z}}$
(i.e.,
$H^1_{\mathbb {Z}}$
(i.e.,
![]() $\langle e_i, e_j \rangle = \langle f_i, f_j \rangle =0$
,
$\langle e_i, e_j \rangle = \langle f_i, f_j \rangle =0$
,
![]() $\langle e_i, f_j \rangle = \delta _{ij}$
). Under the identification
$\langle e_i, f_j \rangle = \delta _{ij}$
). Under the identification
if
![]() $\Phi _1(X_e - X_e^-)$
is non-torsion, there exists elements
$\Phi _1(X_e - X_e^-)$
is non-torsion, there exists elements
![]() $\varphi _1$
,
$\varphi _1$
,
![]() $\varphi _2$
,
$\varphi _2$
,
![]() $\varphi _3 \in S$
such that
$\varphi _3 \in S$
such that
is non-torsion. By renumbering, we may assume that
![]() $\varphi _1$
,
$\varphi _1$
,
![]() $\varphi _2$
,
$\varphi _2$
,
![]() $\varphi _3 \in \{e_i, f_i \mid 1 \leq i \leq 3\}$
. For
$\varphi _3 \in \{e_i, f_i \mid 1 \leq i \leq 3\}$
. For
![]() $i=1, \ldots , k-1$
, we put
$i=1, \ldots , k-1$
, we put
Note that
![]() $i+3 \leq g$
by the assumption. Put
$i+3 \leq g$
by the assumption. Put
![]() $\varphi = \varphi _1 \wedge \cdots \wedge \varphi _{2k+1}$
. Then, by [Reference Otsubo16, Proposition 3.7], we have
$\varphi = \varphi _1 \wedge \cdots \wedge \varphi _{2k+1}$
. Then, by [Reference Otsubo16, Proposition 3.7], we have
 $$ \begin{align*} &k! \cdot \Phi_k(W_{k, e}-W_{k, e}^-)(\varphi) \\ &=k! \cdot \sum_{\sigma} \Phi_1(X_e- X_e^-)(\varphi_{\sigma(1)} \wedge \varphi_{\sigma(2)} \wedge \varphi_{\sigma(3)}) \prod_{i=1}^{k-1} \langle \varphi_{\sigma(2i+2)}, \varphi_{\sigma(2i+3)}\rangle \\ & =k! \cdot \Phi_1(X_e- X_e^-)(\varphi_{1} \wedge \varphi_{2} \wedge \varphi_{3}), \end{align*} $$
$$ \begin{align*} &k! \cdot \Phi_k(W_{k, e}-W_{k, e}^-)(\varphi) \\ &=k! \cdot \sum_{\sigma} \Phi_1(X_e- X_e^-)(\varphi_{\sigma(1)} \wedge \varphi_{\sigma(2)} \wedge \varphi_{\sigma(3)}) \prod_{i=1}^{k-1} \langle \varphi_{\sigma(2i+2)}, \varphi_{\sigma(2i+3)}\rangle \\ & =k! \cdot \Phi_1(X_e- X_e^-)(\varphi_{1} \wedge \varphi_{2} \wedge \varphi_{3}), \end{align*} $$
where
![]() $\sigma $
runs through the elements of the symmetric group
$\sigma $
runs through the elements of the symmetric group
![]() $S_{2k+1}$
such that
$S_{2k+1}$
such that
![]() ${\sigma (1) < \sigma (2) < \sigma (3)}$
,
${\sigma (1) < \sigma (2) < \sigma (3)}$
,
![]() $\sigma (2i+2) < \sigma (2i+3)$
for
$\sigma (2i+2) < \sigma (2i+3)$
for
![]() $1 \leq i \leq k-1$
, and
$1 \leq i \leq k-1$
, and
![]() $\sigma (2i+2) < \sigma (2i+4)$
for
$\sigma (2i+2) < \sigma (2i+4)$
for
![]() $1 \leq i \leq k-2$
. Therefore,
$1 \leq i \leq k-2$
. Therefore,
![]() $\Phi _k(W_{k, e}-W_{k, e}^-)$
is non-torsion.
$\Phi _k(W_{k, e}-W_{k, e}^-)$
is non-torsion.
Corollary 3.2 Let N be an integer which has a prime divisor
![]() $p> 7$
and
$p> 7$
and
![]() $X=F_N$
be the Fermat curve of degree N. Then
$X=F_N$
be the Fermat curve of degree N. Then
![]() $\Phi _k(W_{k, e}-W_{k, e}^-)$
is non-torsion for any
$\Phi _k(W_{k, e}-W_{k, e}^-)$
is non-torsion for any
![]() $e \in F_N$
and
$e \in F_N$
and
![]() $k=1, \ldots , g-2$
.
$k=1, \ldots , g-2$
.
Proof By Proposition 3.1, we are reduced to the case
![]() $k=1$
, which is a theorem of Eskandari and Murty [Reference Eskandari and Murty6, Theorem 1.1].
$k=1$
, which is a theorem of Eskandari and Murty [Reference Eskandari and Murty6, Theorem 1.1].
3.2 Harris-Pulte formula
In this subsection, we recall the Harris-Pulte formula, which is a relation between the Abel-Jacobi image of the Ceresa cycle and an extension class of mixed Hodge structures on the space of quadratic iterated integrals on the curve X.
We put
Then the map
which is obtained by restricting the natural quotient map
![]() $(H^1)^{\otimes 3} \to \wedge ^3H^1$
, is surjective ([Reference Pulte17, Lemma 4.7]), and induces the injective map
$(H^1)^{\otimes 3} \to \wedge ^3H^1$
, is surjective ([Reference Pulte17, Lemma 4.7]), and induces the injective map
Let
![]() $\pi _1(X, e)$
be the fundamental group. Let I be the augmentation ideal of the group ring
$\pi _1(X, e)$
be the fundamental group. Let I be the augmentation ideal of the group ring
![]() $\mathbb {Z}[\pi _1(X, e)]$
– that is, the kernel of the degree map
$\mathbb {Z}[\pi _1(X, e)]$
– that is, the kernel of the degree map
By Chen’s
![]() $\pi _1$
-de Rham theorem,
$\pi _1$
-de Rham theorem,
![]() $\operatorname {Hom}(\mathbb {Z}[\pi _1(X, e)]/I^{s+1}, \mathbb {R})$
is generated by closed iterated integrals of length
$\operatorname {Hom}(\mathbb {Z}[\pi _1(X, e)]/I^{s+1}, \mathbb {R})$
is generated by closed iterated integrals of length
![]() $\leq s$
. Using this, Hain [Reference Hain9] defines a
$\leq s$
. Using this, Hain [Reference Hain9] defines a
![]() $\mathbb {Z}$
-mixed Hodge structure on
$\mathbb {Z}$
-mixed Hodge structure on
![]() $\mathbb {Z}[\pi _1(X, e)]/I^s$
such that the natural map
$\mathbb {Z}[\pi _1(X, e)]/I^s$
such that the natural map
![]() $\mathbb {Z}[\pi _1(X, e)]/I^s \to \mathbb {Z}[\pi _1(X, e)]/I^t$
for
$\mathbb {Z}[\pi _1(X, e)]/I^s \to \mathbb {Z}[\pi _1(X, e)]/I^t$
for
![]() $s \geq t$
is a morphism of mixed Hodge structures. Consider the exact sequence of mixed Hodge structures
$s \geq t$
is a morphism of mixed Hodge structures. Consider the exact sequence of mixed Hodge structures
The map
![]() $\pi _1(X, e) \to I/I^2; \gamma \mapsto \gamma -1$
is well-defined and induces an isomorphism
$\pi _1(X, e) \to I/I^2; \gamma \mapsto \gamma -1$
is well-defined and induces an isomorphism
of Hodge structures of weight
![]() $-1$
. However, the multiplication
$-1$
. However, the multiplication
![]() $I/I^2 \otimes I/I^2 \to I^2/I^3$
induces an isomorphism
$I/I^2 \otimes I/I^2 \to I^2/I^3$
induces an isomorphism
of Hodge structures of weight
![]() $2$
. Taking the dual of (3.1), we have an exact sequence
$2$
. Taking the dual of (3.1), we have an exact sequence
where we put
![]() $L_2(X, e)=\operatorname {Hom}(I/I^3, \mathbb {Z})$
.
$L_2(X, e)=\operatorname {Hom}(I/I^3, \mathbb {Z})$
.
Let
![]() $\infty \neq e$
be another point on X. Put
$\infty \neq e$
be another point on X. Put
![]() $U=X-\{\infty \}$
. We identify
$U=X-\{\infty \}$
. We identify
![]() $H^1(U)$
and
$H^1(U)$
and
![]() $H^1$
via the map induced by the inclusion
$H^1$
via the map induced by the inclusion
![]() $U \subset X$
. Then we can obtain an exact sequence of mixed Hodge structures
$U \subset X$
. Then we can obtain an exact sequence of mixed Hodge structures
similarly as above. We have a commutative diagram

Let
![]() $\mathbb {E}_e$
(resp.
$\mathbb {E}_e$
(resp.
![]() $\mathbb {E}_e^{\infty }$
) be an extension class of the top (resp. bottom) row. We regard
$\mathbb {E}_e^{\infty }$
) be an extension class of the top (resp. bottom) row. We regard
![]() $\mathbb {E}_e$
as an element of
$\mathbb {E}_e$
as an element of
 $$ \begin{align*} \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}( (H^1 \otimes H^1)', H^1) &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}((H^1)^{\vee} \otimes (H^1 \otimes H^1)', \mathbb{Z}(0)) \\ &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}(H^1 \otimes (H^1 \otimes H^1)', \mathbb{Z}(-1)), \end{align*} $$
$$ \begin{align*} \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}( (H^1 \otimes H^1)', H^1) &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}((H^1)^{\vee} \otimes (H^1 \otimes H^1)', \mathbb{Z}(0)) \\ &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}(H^1 \otimes (H^1 \otimes H^1)', \mathbb{Z}(-1)), \end{align*} $$
and
![]() $\mathbb {E}_e^{\infty }$
as an element of
$\mathbb {E}_e^{\infty }$
as an element of
 $$ \begin{align*} \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}( H^1 \otimes H^1, H^1) &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}((H^1)^{\vee} \otimes H^1 \otimes H^1, \mathbb{Z}(0)) \\ &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}(H^1 \otimes H^1 \otimes H^1, \mathbb{Z}(-1)). \end{align*} $$
$$ \begin{align*} \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}( H^1 \otimes H^1, H^1) &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}((H^1)^{\vee} \otimes H^1 \otimes H^1, \mathbb{Z}(0)) \\ &\cong \mathrm{Ext}_{\mathrm{MHS}(\mathbb{Z})}(H^1 \otimes H^1 \otimes H^1, \mathbb{Z}(-1)). \end{align*} $$
Here, we used the Poincaré duality
![]() $H^1(1) \cong (H^1)^{\vee }$
. One sees that
$H^1(1) \cong (H^1)^{\vee }$
. One sees that
![]() $\mathbb {E}_e$
is the restriction of
$\mathbb {E}_e$
is the restriction of
![]() $\mathbb {E}_e^{\infty }$
to
$\mathbb {E}_e^{\infty }$
to
![]() $H^1 \otimes (H^1 \otimes H^1)'$
. Then Harris’s formula [Reference Harris10, Section 4], reworked by Pulte [Reference Pulte17, Theorem 4.10], is
$H^1 \otimes (H^1 \otimes H^1)'$
. Then Harris’s formula [Reference Harris10, Section 4], reworked by Pulte [Reference Pulte17, Theorem 4.10], is
under the identification
![]() $J_1(\operatorname {Jac}(X))=\mathrm {Ext}_{\mathrm {MHS}(\mathbb {Z})}(\wedge ^3 H^1, \mathbb {Z}(-1))$
.
$J_1(\operatorname {Jac}(X))=\mathrm {Ext}_{\mathrm {MHS}(\mathbb {Z})}(\wedge ^3 H^1, \mathbb {Z}(-1))$
.
3.3 The decomposition of
 $(H^1)^{\otimes 3}$
$(H^1)^{\otimes 3}$
In this subsection, for a
![]() $\mathbb {Z}$
-mixed Hodge structure H, we consider the image of H under the forgetful functor
$\mathbb {Z}$
-mixed Hodge structure H, we consider the image of H under the forgetful functor
![]() $\mathrm {MHS}(\mathbb {Z}) \to \mathrm {MHS(\mathbb {Q})}$
, which we denote by the same letter. The Hodge structure
$\mathrm {MHS}(\mathbb {Z}) \to \mathrm {MHS(\mathbb {Q})}$
, which we denote by the same letter. The Hodge structure
![]() $(H^1)^{\otimes 3}$
can be decomposed in MHS(
$(H^1)^{\otimes 3}$
can be decomposed in MHS(
![]() $\mathbb {Q}$
) as follows. Let
$\mathbb {Q}$
) as follows. Let
![]() $\xi _{\Delta } \in H^1 \otimes H^1$
be the Künneth component of the Hodge class of the diagonal of X in
$\xi _{\Delta } \in H^1 \otimes H^1$
be the Künneth component of the Hodge class of the diagonal of X in
![]() $H^2(X \times X)$
. Then we have a decomposition
$H^2(X \times X)$
. Then we have a decomposition
Since the Mumford-Tate group of
![]() $H^1$
is reductive, the map
$H^1$
is reductive, the map
![]() $\phi $
admits a section
$\phi $
admits a section
![]() $\sigma $
in MHS(
$\sigma $
in MHS(
![]() $\mathbb {Q}$
), and we have
$\mathbb {Q}$
), and we have
Let
![]() $\overline {\xi }_{\Delta }$
be the image of
$\overline {\xi }_{\Delta }$
be the image of
![]() $\xi _{\Delta }$
in
$\xi _{\Delta }$
in
![]() $\wedge ^2H^1$
. Then we have a decomposition in MHS(
$\wedge ^2H^1$
. Then we have a decomposition in MHS(
![]() $\mathbb {Q}$
)
$\mathbb {Q}$
)
where the last summand (primitive part) is the kernel of the map
![]() $\wedge ^3H^1 \to \wedge ^{2g-1}H^1$
given by wedging by
$\wedge ^3H^1 \to \wedge ^{2g-1}H^1$
given by wedging by
![]() $\overline {\xi }_{\Delta }^{g-2}$
(cf. [Reference Eskandari and Murty7, Section 4.2]). We put
$\overline {\xi }_{\Delta }^{g-2}$
(cf. [Reference Eskandari and Murty7, Section 4.2]). We put
![]() $\mathbb {E} :=\mathbb {E}_e |_{\sigma ((\wedge ^3H^1)_{\mathrm {prim}})}$
. Then
$\mathbb {E} :=\mathbb {E}_e |_{\sigma ((\wedge ^3H^1)_{\mathrm {prim}})}$
. Then
![]() $\mathbb {E}$
is independent of the choice of e ([Reference Pulte17, Theorem 3.9] and [Reference Harris10]).
$\mathbb {E}$
is independent of the choice of e ([Reference Pulte17, Theorem 3.9] and [Reference Harris10]).
Proposition 3.3
-
(i) Suppose that
 $-2g[\infty ]+2[e] +K=0$
. Then
$-2g[\infty ]+2[e] +K=0$
. Then
 $\mathbb {E}_{e}^{\infty } =0$
if and only if
$\mathbb {E}_{e}^{\infty } =0$
if and only if
 $\mathbb {E}_{e} =0$
.
$\mathbb {E}_{e} =0$
. -
(ii) Suppose that
 $(2g-2)[e]-K =0$
. Then
$(2g-2)[e]-K =0$
. Then
 $\mathbb {E}_{e}=0$
if and only if
$\mathbb {E}_{e}=0$
if and only if
 $\mathbb {E}=0$
.
$\mathbb {E}=0$
.
Proof (i) The statement follows from that
![]() $\mathbb {E}_e^{\infty }|_{H^1 \otimes (H^1 \otimes H^1)'}=\mathbb {E}_e$
and a result of Kaenders [Reference Kaenders13, Theorem 1.2] that
$\mathbb {E}_e^{\infty }|_{H^1 \otimes (H^1 \otimes H^1)'}=\mathbb {E}_e$
and a result of Kaenders [Reference Kaenders13, Theorem 1.2] that
under the identification (cf. [Reference Eskandari and Murty7, Section 4.3.1])
(ii) The statement follows from that results of Harris [Reference Harris10, Section 3] and Pulte [Reference Pulte17, Theorem 4.10]] that
![]() $\mathbb {E}_e|_{\operatorname {ker}(\phi )} \in \mathrm { Ext}_{\mathrm {MHS}(\mathbb {Q})}(\ker (\phi ), \mathbb {Q}(-1))$
is zero, and Pulte [Reference Pulte17, Corollary 6.7] that
$\mathbb {E}_e|_{\operatorname {ker}(\phi )} \in \mathrm { Ext}_{\mathrm {MHS}(\mathbb {Q})}(\ker (\phi ), \mathbb {Q}(-1))$
is zero, and Pulte [Reference Pulte17, Corollary 6.7] that
under the identification (cf. [Reference Eskandari and Murty7, Section 4.3.3])
3.4 Darmon-Rotger-Sols formula
Let
![]() $\Delta \in \operatorname {CH}_1(X \times X)$
be the diagonal of X and
$\Delta \in \operatorname {CH}_1(X \times X)$
be the diagonal of X and
be the projection to the i-th component. For
![]() $Z \in \operatorname {CH}_1(X \times X)$
, put
$Z \in \operatorname {CH}_1(X \times X)$
, put
 $$ \begin{align*} Z_{12}&=(p_1)_*(Z \cdot \Delta)=(p_2)_*(Z \cdot \Delta), \\ Z_1&=(p_1)_*(Z \cdot (X \times \{e\})), \quad Z_2=(p_2)_*(Z \cdot (\{e\} \times X)) \in \operatorname{CH}_0(X). \end{align*} $$
$$ \begin{align*} Z_{12}&=(p_1)_*(Z \cdot \Delta)=(p_2)_*(Z \cdot \Delta), \\ Z_1&=(p_1)_*(Z \cdot (X \times \{e\})), \quad Z_2=(p_2)_*(Z \cdot (\{e\} \times X)) \in \operatorname{CH}_0(X). \end{align*} $$
Put
Then the point
![]() $P_Z$
is related to the extension
$P_Z$
is related to the extension
![]() $\mathbb {E}_e^{\infty }$
as follows. Let
$\mathbb {E}_e^{\infty }$
as follows. Let
![]() $\xi _Z$
be the
$\xi _Z$
be the
![]() $H^1 \otimes H^1$
-Künneth component of the class of Z in
$H^1 \otimes H^1$
-Künneth component of the class of Z in
![]() $H^2(X \times X)$
. Consider the map
$H^2(X \times X)$
. Consider the map
where the first arrow is the pullback along the morphism
![]() $H^1(-1) \to (H^1)^{\otimes 3}$
defined by
$H^1(-1) \to (H^1)^{\otimes 3}$
defined by
![]() $\omega \mapsto \omega \otimes \xi _Z$
. Then we have the following.
$\omega \mapsto \omega \otimes \xi _Z$
. Then we have the following.
Proposition 3.4 [Reference Darmon, Rotger and Sols5, Corollary 2.6]
For any
![]() $Z \in \operatorname {CH}_1(X \times X)$
, we have
$Z \in \operatorname {CH}_1(X \times X)$
, we have
in
![]() $\operatorname {Jac}(X)$
.
$\operatorname {Jac}(X)$
.
4 Proof of Theorem 1.1
There are
![]() $3N$
points on
$3N$
points on
![]() $F_N$
$F_N$
where we put
![]() $\xi _N=\exp (\pi i /N)$
. Fix
$\xi _N=\exp (\pi i /N)$
. Fix
![]() $P_0$
as the base point; then the above points are torsion points in
$P_0$
as the base point; then the above points are torsion points in
![]() $\operatorname {Jac}(F_N)$
[Reference Gross and Rohrlich8]. Therefore, for the base point
$\operatorname {Jac}(F_N)$
[Reference Gross and Rohrlich8]. Therefore, for the base point
![]() $\pi _N^{a, b}(P_0)$
, the images of these points under
$\pi _N^{a, b}(P_0)$
, the images of these points under
![]() $(\pi _N^{a, b})_*$
are also torsion in
$(\pi _N^{a, b})_*$
are also torsion in
![]() $\operatorname {Jac}(C_N^{a, b})$
. We shall continue to use the notation as in the previous section, specializing
$\operatorname {Jac}(C_N^{a, b})$
. We shall continue to use the notation as in the previous section, specializing
![]() $X=C_N^{a, b}$
,
$X=C_N^{a, b}$
,
![]() $e=\pi _N^{a, b}(P_0)$
and
$e=\pi _N^{a, b}(P_0)$
and
![]() ${\infty = \pi _N^{a, b}(Q_0)}$
.
${\infty = \pi _N^{a, b}(Q_0)}$
.
Lemma 4.1 Let
![]() $K_C$
(resp. g) be the canonical divisor (resp. genus) of
$K_C$
(resp. g) be the canonical divisor (resp. genus) of
![]() $C_N^{a, b}$
. Then
$C_N^{a, b}$
. Then
![]() ${K_C-(2g-2)[e]}$
,
${K_C-(2g-2)[e]}$
,
![]() $K_C-2g[\infty ]+2[e] \in \operatorname {Jac}(C_N^{a, b})$
are torsion points.
$K_C-2g[\infty ]+2[e] \in \operatorname {Jac}(C_N^{a, b})$
are torsion points.
Proof Since
and
![]() $[\infty ]-[e]$
is a torsion point, it suffices to show that
$[\infty ]-[e]$
is a torsion point, it suffices to show that
![]() $K_C -(2g-2)[e]$
is a torsion point. Let
$K_C -(2g-2)[e]$
is a torsion point. Let
![]() $K_F$
be the canonical divisor of
$K_F$
be the canonical divisor of
![]() $F_N$
and
$F_N$
and
![]() $R_{\pi _N^{a, b}}$
be the ramification divisor of
$R_{\pi _N^{a, b}}$
be the ramification divisor of
![]() $\pi _N^{a, b}$
; that is,
$\pi _N^{a, b}$
; that is,
 $$ \begin{align*} &K_F=(N-1) \sum_{i=0}^{N-1}Q_i -2 \sum_{i=0}^{N-1} R_i, \\ &R_{\pi_N^{a, b}}=(\gcd(N, a)-1)\sum_{i=0}^{N-1} P_i + (\gcd(N, b)-1)\sum_{i=0}^{N-1} Q_i +(\gcd(N, a+b)-1)\sum_{i=0}^{N-1} R_i. \end{align*} $$
$$ \begin{align*} &K_F=(N-1) \sum_{i=0}^{N-1}Q_i -2 \sum_{i=0}^{N-1} R_i, \\ &R_{\pi_N^{a, b}}=(\gcd(N, a)-1)\sum_{i=0}^{N-1} P_i + (\gcd(N, b)-1)\sum_{i=0}^{N-1} Q_i +(\gcd(N, a+b)-1)\sum_{i=0}^{N-1} R_i. \end{align*} $$
Then we have
up to principal divisor (cf. [Reference Hartshorne11, Proposition 2.3, Chap.IV]). Therefore, we have
in
![]() $\operatorname {Jac}(C_N^{a, b})$
. Since
$\operatorname {Jac}(C_N^{a, b})$
. Since
![]() $P_i$
,
$P_i$
,
![]() $Q_i$
, and
$Q_i$
, and
![]() $R_i$
are torsion in
$R_i$
are torsion in
![]() $\operatorname {Jac}(F_N)$
,
$\operatorname {Jac}(F_N)$
,
![]() $K_F -R_{\pi _N^{a, b}}-(2g-2)N[P_0]$
is torsion, which finishes the proof.
$K_F -R_{\pi _N^{a, b}}-(2g-2)N[P_0]$
is torsion, which finishes the proof.
Proof of Theorem 1.1
First, by Proposition 3.1, it suffices to show the case when
![]() $k=1$
. Secondly, consider the map
$k=1$
. Secondly, consider the map
Let
![]() $\langle a \rangle \in \{0, \ldots , p-1\}$
be the representative of a. Then f descends to a map
$\langle a \rangle \in \{0, \ldots , p-1\}$
be the representative of a. Then f descends to a map
![]() $\overline {f} \colon C^{a, b}_N \to C^{\langle a \rangle , \langle b \rangle }_p$
. Since
$\overline {f} \colon C^{a, b}_N \to C^{\langle a \rangle , \langle b \rangle }_p$
. Since
we are reduced to the case when
![]() $N=p$
.
$N=p$
.
By Lemma 4.1 and Proposition 3.3, it suffices to show that, for the specific choices of e and
![]() $\infty $
as above, the element
$\infty $
as above, the element
![]() $\mathbb {E}^{\infty }_{e} \in \mathrm {Ext}_{\mathrm {MHS}(\mathbb {Q})}(H^1 \otimes H^1 \otimes H^1, \mathbb {Q}(-1))$
is nonzero. By Lemma 2.1, the automorphism
$\mathbb {E}^{\infty }_{e} \in \mathrm {Ext}_{\mathrm {MHS}(\mathbb {Q})}(H^1 \otimes H^1 \otimes H^1, \mathbb {Q}(-1))$
is nonzero. By Lemma 2.1, the automorphism
![]() $\beta $
of
$\beta $
of
![]() $F_p$
descends to an automorphism
$F_p$
descends to an automorphism
![]() $\widetilde {\beta }$
of
$\widetilde {\beta }$
of
![]() $C_p^{a, b}$
; let Z be the graph of
$C_p^{a, b}$
; let Z be the graph of
![]() $\widetilde {\beta }$
. Since
$\widetilde {\beta }$
. Since
![]() $[\infty ] - [e]$
is torsion, it suffices to show that
$[\infty ] - [e]$
is torsion, it suffices to show that
![]() $P_Z$
is non-torsion by Proposition 3.4. Since
$P_Z$
is non-torsion by Proposition 3.4. Since
![]() $\widetilde {\beta } \circ \pi _p^{a, b}=\pi _p^{a, b}\circ \beta $
and
$\widetilde {\beta } \circ \pi _p^{a, b}=\pi _p^{a, b}\circ \beta $
and
![]() $\widetilde {\beta }$
has two fixed points by Lemma 2.3, we have
$\widetilde {\beta }$
has two fixed points by Lemma 2.3, we have
 $$ \begin{align*} P_Z&=([\pi_p^{a, b}(S)]+[\pi_p^{a, b}(\overline{S})]-2[e])-([\widetilde{\beta}(e)]+[\widetilde{\beta}^{-1}(e)]-2[e]) \\ &=(\pi_p^{a, b})_*(([S]+[\overline{S}]-2[P_0])-([\beta(P_0)]+[\beta^{-1}(P_0)]-2[P_0])). \end{align*} $$
$$ \begin{align*} P_Z&=([\pi_p^{a, b}(S)]+[\pi_p^{a, b}(\overline{S})]-2[e])-([\widetilde{\beta}(e)]+[\widetilde{\beta}^{-1}(e)]-2[e]) \\ &=(\pi_p^{a, b})_*(([S]+[\overline{S}]-2[P_0])-([\beta(P_0)]+[\beta^{-1}(P_0)]-2[P_0])). \end{align*} $$
The point
![]() $[\beta (P_0)]+[\beta ^{-1}(P_0)]-2[P_0]$
is a torsion point on
$[\beta (P_0)]+[\beta ^{-1}(P_0)]-2[P_0]$
is a torsion point on
![]() $\operatorname {Jac}(F_p)$
; hence,
$\operatorname {Jac}(F_p)$
; hence,
![]() $(\pi _p^{a, b})_*([\beta (P_0)]+[\beta ^{-1}(P_0)]-2[P_0])$
is a torsion point on
$(\pi _p^{a, b})_*([\beta (P_0)]+[\beta ^{-1}(P_0)]-2[P_0])$
is a torsion point on
![]() $\operatorname {Jac}(C_p^{a, b})$
. However, since
$\operatorname {Jac}(C_p^{a, b})$
. However, since
![]() $a-b, a+2b, 2a+b \not \equiv 0 \ \ \pmod {p}$
by the assumption
$a-b, a+2b, 2a+b \not \equiv 0 \ \ \pmod {p}$
by the assumption
![]() $a^2+ab+b^2 \equiv 0 \ \ \pmod {p}$
, the point
$a^2+ab+b^2 \equiv 0 \ \ \pmod {p}$
, the point
is non-torsion by Theorem 2.4. Therefore, the point
![]() $P_Z$
is non-torsion, which finishes the proof.
$P_Z$
is non-torsion, which finishes the proof.
Acknowledgements
The author would like to sincerely thank Noriyuki Otsubo for valuable discussions and his careful reading on a draft of this paper. He would like to thank Yoshinosuke Hirakawa for valuable discussions and many helpful comments. He also thanks Payman Eskandari, Yuki Goto, and Ryutaro Sekigawa for valuable discussions. This paper is a part of the outcome of research performed under Waseda University Grant for Special Research Projects (Project number: 2023C-274) and Kakenhi Applicants (Project number: 2023R-044).