Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-17T13:22:42.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonoscillation of Second Order Superlinear Differential Equations

Published online by Cambridge University Press:  20 November 2018

L. H. Erbe ,
H. X. Xia  and
J. H. Wu
L. H. Erbe
Affiliation:
Department of Mathematics, University of Alberta Edmonton, Alberta T6G 2G1
H. X. Xia
Affiliation:
Department of Mathematics, University of Alberta Edmonton, Alberta T6G 2G1
J. H. Wu
Affiliation:
Department of Mathematics, York University, North York, Ontario M3J 1P3
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Some sufficient conditions are given for all solutions of the nonlinear differential equation y″(x) +p(x)f(y) = 0 to be nonoscillatory, where p is positive and

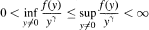
for a quotient γ of odd positive integers, γ > 1.

Keywords

34C15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 2 , 01 June 1994 , pp. 178 - 186
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Atkinson, F. V., On second order nonlinear oscillations, Pacific J. Math. 5(1955), 643–647.Google Scholar
2. Belohorec, S., Oscillatory solutions of certain nonlinear differential equations of second order, Mat. Casopis Sloven, Akad. Vied. 11(1961), 250–255.Google Scholar
3. Belohorec, S., On some properties of the equation y″(x)+f(x)yα(x) = 0, 0 < α <1, Mat. Casopis Solven. Akad. Vied. 17(1967), 10–19.Google Scholar
4. Chiou, K. L., The existence of oscillatory solutions for the equation Proc. Amer. Math. Soc. 35(1972), 120–122.Google Scholar
5. Chiou, K. L., A nonoscillation theorem for the superlinear case of second order differential equations y″ + yF(y2,x) =0, SIAM J. Appl. Math. 23(1972), 456–459.Google Scholar
6. Coffman, C. V. and Wong, J. S. W., On a second order nonlinear oscillation problem, Trans. Amer. Math. Soc. 147(1970), 357–366.Google Scholar
7. Coffman, C. V. and Wong, J. S. W., Oscillation and nonoscillation theorems for the generalized Emden-Fowler equations, Trans. Amer. Math. Soc. 167(1973), 399–434.Google Scholar
8. Erbe, L. H., Nonoscillation criteria for second order nonlinear differential equations, J. Math. Anal. Appl. 108(1985), 515–527.Google Scholar
9. Erbe, L. H., Oscillation and nonoscillationpropertiesfor second order nonlinear differential equations, Equadiff 82, Wurzburg, 1982. Lecture Notes in Math., Springer, 1983, 168–176.Google Scholar
10. Erbe, L. H. and Hong Lu, Nonoscillation theorems for second order nonlinear differential equations, Funkcial. Ekvac. 33(1990), 227–244.Google Scholar
11. Erbe, L. H. and Muldowney, J. S., On the existence of oscillatory solutions to nonlinear differential equations, Ann. Math. Pura. Appl. 59(1976), 23–37.Google Scholar
12. Erbe, L. H. and Muldowney, J. S., Nonoscillation results for second order nonlinear differential equations, Rocky Mountain J. Math. 12(1982), 635–642.Google Scholar
13. Fowler, R. H., Further studies of Emden 's and similar differential equations, Quart. J. Math. 2(1931 ), 259– 288.Google Scholar
14. Gidas, B., Ni, W. M. and Nirenberg, L., Symmetry and related properties via the maximum principle, Comm. Math. Phys. 68(1979), 209–243.Google Scholar
15. Kaper, H. G. and Kwong, M. K., A non-oscillation theorem for the Emden-Fowler equation: ground states for semilinear elliptic equations with critical exponents, J. Differential Equations 75(1988), 158–185.Google Scholar
16. Nehari, Z., A nonlinear oscillation theorem, Duke Math. J. 42(1975), 183–189. 17 , Mathematical Reviews, (11661), 48, (1974).Google Scholar
18. Wong, J. S. W., On second order nonlinear oscillation, Funkcial. Ekvac. 11(1968), 207–234.Google Scholar
19. Wong, J. S. W., Oscillation theorems for second order nonlinear differential equations, Bull. Inst. Math. Acad. Sinica 3(1975), 283–309.Google Scholar
20. Wong, J. S. W., On the generalized Emden-Fowler equation, SIAM Rev. 17(1975), 339–360.Google Scholar