Published online by Cambridge University Press: 20 November 2018
Let Hp(0<p≤∞) be the Hardy class of functions holomorphic in D={|z|<1}, and let f be a function holomorphic in D. It follows from the well known theorem [1, Theorem 3.11, p. 42] that if (I) 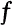 , then (II) f can be extended continuously to the closed disk {|z|≤1}, and consequently, (III) f is normal in D in the sense of O. Lehto and K. I. Virtanen [2]. Since there is a considerable gap between (II) and (III), one would suspect that the condition (I) might be much stronger than necessary to obtain the conclusion (III). However, it is curious that the implication (I)⇒(III) is sharp as the following theorem shows.
, then (II) f can be extended continuously to the closed disk {|z|≤1}, and consequently, (III) f is normal in D in the sense of O. Lehto and K. I. Virtanen [2]. Since there is a considerable gap between (II) and (III), one would suspect that the condition (I) might be much stronger than necessary to obtain the conclusion (III). However, it is curious that the implication (I)⇒(III) is sharp as the following theorem shows.