Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T04:37:44.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Left-Orderable 3-Manifold Groups

Published online by Cambridge University Press:  20 November 2018

Mieczysław K. Dąbkowski ,
Józef H. Przytycki  and
Amir A. Togha
Mieczysław K. Dąbkowski
Affiliation:
Mathematical Science Department, The Univesity of Texas at Dallas, Richardson, TX 75803-0688, U.S.A. e-mail: [email protected]
Józef H. Przytycki
Affiliation:
Department of Mathematics, The GeorgeWashington University, Washington, D.C. 20052, U.S.A. e-mail: [email protected]
Amir A. Togha
Affiliation:
Department of Mathematics, The GeorgeWashington University, Washington, D.C. 20052, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

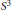We show that several torsion free 3-manifold groups are not left-orderable. Our examples are groups of cyclic branched coverings of ${{S}^{3}}$ branched along links. The figure eight knot provides simple nontrivial examples. The groups arising in these examples are known as Fibonacci groups which we show not to be left-orderable. Many other examples of non-orderable groups are obtained by taking 3-fold branched covers of 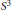${{S}^{3}}$ branched along various hyperbolic 2-bridge knots. The manifold obtained in such a way from the 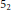${{5}_{2}}$ knot is of special interest as it is conjectured to be the hyperbolic 3-manifold with the smallest volume.

Keywords

57M2557M1220F60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 1 , 01 March 2005 , pp. 32 - 40
Copyright
Copyright © Canadian Mathematical Society 2005

References

[Bo] Boileau, M., Geometrization of 3-manifolds with symmetries. Advanced Course on Geometric 3-Manifolds. A Euro Summer School, September, 2002. http://www.crm.es./Publications/Quaderns/Quadern25-1.pdf Google Scholar
[BRW] Boyer, S., Rolfsen, D., and Wiest, B., Orderable 3-manifold groups. Ann. Inst. Fourier, to appear. http://front.math.ucdavis.edu/math.GT/0211110 Google Scholar
[B-Z] Burde, G. and Zieschang, H., Knots, de Gruyter Studies in Mathematics 5, 1985. Second ed., Walter de Gruyter, 2003.Google Scholar
[C-D] Calegari, D. and Dunfield, N. M., Laminations and groups of homeomorphisms of the circle. Invent.Math. 152(2003), 149–204.Google Scholar
[Cr] Crowell, R., The derived group of a permutation representation. Adv. in Math. 53(1984), 99–124.Google Scholar
[DDRW] Dehornoy, P., Dynnikov, I., Rolfsen, D., and Wiest, B., Why are braids orderable? Panoramas et Synthèses [Panoramas and Syntheses], 14. Société Mathématique de France, Paris, 2002.Google Scholar
[H-W] Hantzsche, W. and Wendt, H., Dreidimensional euklidische Raumformen. Math. Annalen 110(1934-35), 593–611.Google Scholar
[HLM] Hilden, H. M., Lozano, M. T., and Montesinos-Amilibia, J. M., The Arithmeticity of the figure eight knot orbifolds. In: Topology ‘90, (eds. Apanasov, B., Neumann, W., Reid, A., and Siebenmann, L.), de Gruyter, Berlin, 1992, pp. 169–183.Google Scholar
[Ho] Hodgson, C. D., Degeneration and regeneration of hyperbolic structures on three-manifolds. Thesis, Princeton University, 1986.Google Scholar
[H-S] Howie, J. and Short, H., The band-sum problem. J. LondonMath. Soc. (2) 31(1985), 571–576.Google Scholar
[Ki] Kirby, R., Problems in low-dimensional topology. AMS/IP Stud. Adv. Math. 2.2(1997), 35–473.Google Scholar
[M-V] Mulazzani, M. and Vesnin, A., Generalized Takahashi manifolds. Osaka J. Math. 39(2002), 705–721.Google Scholar