Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T20:26:09.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-complemented Spaces of Operators, Vector Measures, and co

Published online by Cambridge University Press:  20 November 2018

Paul Lewis  and
Polly Schulle
Paul Lewis
Affiliation:
Department of Mathematics, University of North Texas, Denton, TX 76203-1430 USAe-mail: [email protected]
Polly Schulle
Affiliation:
Department of Mathematics, Richland College, Dallas, TX 75243-2199 USAe-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Banach spaces 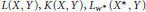$L(X,Y),K(X,Y),{{L}_{{{w}^{*}}}}({{X}^{*}},Y)$, and 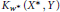${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ are studied to determine when they contain the classical Banach spaces 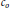${{c}_{o}}$ or 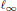${{l}_{\infty }}$. The complementation of the Banach space 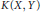$K(X,Y)$ in 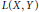$L(X,Y)$ is discussed as well as what impact this complementation has on the embedding of 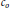${{c}_{o}}$ or 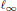${{l}_{\infty }}$ in 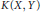$K(X,Y)$ or 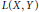$L(X,Y)$. Results of Kalton, Feder, and Emmanuele concerning the complementation of 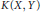$K(X,Y)$ in 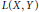$L(X,Y)$ are generalized. Results concerning the complementation of the Banach space 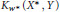${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ in 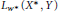${{L}_{{{w}^{*}}}}({{X}^{*}},Y)$ are also explored as well as how that complementation affects the embedding of 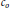${{c}_{o}}$ or 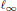${{l}_{\infty }}$ in 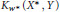${{K}_{{{w}^{*}}}}({{X}^{*}},Y)$ or 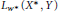${{L}_{{{w}^{*}}}}({{X}^{*}},Y)$. The 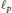${{l}_{p}}$ spaces for 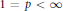$1\,=\,p\,<\,\infty $ are studied to determine when the space of compact operators from one 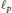${{l}_{p}}$ space to another contains 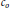${{c}_{o}}$. The paper contains a new result which classifies these spaces of operators. A new result using vector measures is given to provide more efficient proofs of theorems by Kalton, Feder, Emmanuele, Emmanuele and John, and Bator and Lewis.

Keywords

46B20spaces of operatorscompact operatorscomplemented subspacesw* – w-compact operators
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 548 - 554
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bator, E. and Lewis, P., Complemented spaces of operators. Bull. Polish Acad. Sci. Math. 50(2002), no. 4, 413–416.Google Scholar
[2] Diestel, J., Sequences and Series in Banach Spaces, Graduate Texts in Mathematics 92. Springer-Verlag, New York, 1984.Google Scholar
[3] Diestel, J. and Uhl, J. J. Jr., Vector Measures. Mathematical Surveys 15. American Mathematical Society, Providence, RI, 1977.Google Scholar
[4] Drewnowski, L., Copies of ℓ∞in an operator space. Math. Proc. Camb. Philos. Soc. 108(1990), no. 3, 523–526. http://dx.doi.org/10.1017/S0305004100069401 Google Scholar
[5] Emmanuele, G., A remark on the containment of co in the space of compact operators. Math. Proc. Camb. Philos. Soc. 111(1992), no. 2, 331–335. http://dx.doi.org/10.1017/S0305004100075435 Google Scholar
[6] Emmanuele, G., and John, K., Uncomplementability of spaces of compact operators in larger spaces of operators. Czechoslovak Math. J. 47(122)(1997), no. 1, 19–31. http://dx.doi.org/10.1023/A:1022483919972 Google Scholar
[7] Feder, M., On subspaces of spaces with an unconditional basis and spaces of operators. Illinois J. Math. 24(1980), no. 2, 196–206.Google Scholar
[8] Feder, M., On the non-existence of a projection onto the space of compact operators. Canad. Math. Bull. 25(1982), no. 1, 78–81. http://dx.doi.org/10.4153/CMB-1982-011-0 Google Scholar
[9] Ghenciu, I. and Lewis, P., Unconditional convergence in the strong operator topology and ℓ∞ Glasgow Math. J., First View Articles, available on CJO, March 10, 2011. http://dx.doi.org/10.1017/S0017089511000152 Google Scholar
[10] John, K., On the uncomplemented subspace K(X, Y) . Czechoslovak Math. J. 42(117)(1992), no. 1, 167–173.Google Scholar
[11] Kalton, N., Spaces of compact operators. Math. Ann. 208(1974), 267–278. http://dx.doi.org/10.1007/BF01432152 Google Scholar
[12] Lewis, P., Spaces of operators and co. Studia Math. 145(2001), no. 3, 213–218. http://dx.doi.org/10.4064/sm145-3-3 Google Scholar
[13] Ruess, W., Duality and geometry of spaces of compact operators. In: Functional Analysis: Surveys and Recent Results III. North-Holland Math. Studies 90. North-Holland, Amsterdam, 1984, pp. 59–78.Google Scholar
[14] Schlumprecht, T., Limited Sets in Banach Spaces Dissertation, Munich, 1987.Google Scholar
[15] Singer, I., Bases in Banach Spaces. II. Springer-Verlag, Berlin, 1981.Google Scholar