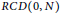Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mondino, Andrea
and
Wei, Guofang
2019.
On the universal cover and the fundamental group of an RCD*(K,N)-space.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 753,
p.
211.