Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T20:52:53.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Near Triangularizability Implies Triangularizability

Published online by Cambridge University Press:  20 November 2018

Bamdad R. Yahaghi
Bamdad R. Yahaghi*
Affiliation:
Department of Mathematics University of Toronto, Toronto, Ontario M5S 3G3, e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider collections of compact operators on a real or complex Banach space including linear operators on finite-dimensional vector spaces. We show that such a collection is simultaneously triangularizable if and only if it is arbitrarily close to a simultaneously triangularizable collection of compact operators. As an application of these results we obtain an invariant subspace theorem for certain bounded operators. 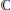We further prove that in finite dimensions near reducibility implies reducibility whenever the ground field is $\mathbb{R}$ or $\mathbb{C}$.

Keywords

47A1547D0320M20Linear transformationCompact operatorTriangularizabilityBanach spaceHilbert space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 2 , 01 June 2004 , pp. 298 - 313
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Bollobás, B., Linear analysis. Cambridge University Press, Cambridge, 1990.Google Scholar
[2] Conway, J. B., A course in functional analysis.Second edition. Springer Verlag, New York, 1990.Google Scholar
[3] Dunford, N. and Schwartz, J. T., Linear operators. Part II: spectral theory. John Wiley, New York, 1963.Google Scholar
[4] Hoffman, K. and Kunze, R., Linear algebra. Second edition, Prenctice-Hall, Englewood Cliffs, New Jersey, 1971.Google Scholar
[5] Halperin, I. and Rosenthal, P., Burnside's theorem on algebras of matrices. Amer.Math. Monthly 87(1980), 810.Google Scholar
[6] Jafarian, A. A., Radjavi, H., Rosenthal, P., and Sourour, A. R., Simultaneous triangularizability, near commutativity, and Rota's theorem. Trans. Amer.Math. Soc. 347 (1995), 2191–2199.Google Scholar
[7] Lang, S., Algebra. Third edition, Springer-Verlag, New York, 2002.Google Scholar
[8] Radjavi, H., On the reduction and triangularization of semigroups of operators. J. Operator Theory 13 (1985), 63–71.Google Scholar
[9] Radjavi, H. and Rosenthal, P., Simultaneous triangularization Springer Verlag, New York, 2000.Google Scholar
[10] Yahaghi, B. R., On semigroups of matrices with traces or inner eigenvalues in a subfield, to be submitted.Google Scholar
[11] Yahaghi, B. R., On simultaneous triangularization of collections of compact operators, submitted.Google Scholar
[12] Yahaghi, B. R., On injective or dense-range operators leaving a given chain of subspaces invariant, to appear in the Proceedings of American Mathematical Scociety.Google Scholar
[13] Yahaghi, B. R., Reducibility results on operator semigroups, Ph.D. Thesis, Dalhousie University, Halifax, 2002.Google Scholar