Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T04:07:47.905Z Has data issue: false hasContentIssue false
  • English
  • Français

A Multivalued Nonlinear System with the Vector p-Laplacian on the Semi-Infinity Interval

Published online by Cambridge University Press:  20 November 2018

Michael E. Filippakis  and
Nikolaos S. Papageorgiou
Michael E. Filippakis
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus, Athens 15780, Greece e-mail: [email protected] e-mail: [email protected]
Nikolaos S. Papageorgiou
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus, Athens 15780, Greece e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a second order nonlinear system driven by the vector 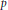$p$-Laplacian, with a multivalued nonlinearity and defined on the positive time semi-axis 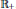${{\mathbb{R}}_{+}}.$ Using degree theoretic techniques we solve an auxiliary mixed boundary value problem defined on the finite interval 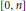$\left[ 0,\,n \right]$ and then via a diagonalization method we produce a solution for the original infinite time horizon system.

Keywords

34A60semi-infinity intervalvectorp-Laplacianmultivalued nonlinearfixed point indexHartman conditioncompletely continuous map
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 2 , 01 June 2008 , pp. 217 - 228
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Agarwal, R. and O’Regan, D., Boundary value problems of nonsingular type on the semi-infinity interval. Tohoku Math. J. 51(1999), no. 3, 391–397.Google Scholar
[2] Bader, R., A topological fixed point index theory for evolution inclusions. Z. Anal. Anwendungen 20(2001), no. 1, 3–15.Google Scholar
[3] Constantin, A., On an infinite interval boundary value problem. Ann. Mat. Pura Appl. 176(1999), 379–394.Google Scholar
[4] Denkowski, Z., Migórski, S., and Papageorgiou, N. S., An Introduction to Nonlinear Analysis: Theory. Kluwer Academic, Boston, 2003.Google Scholar
[5] Denkowski, Z., Migórski, S., and Papageorgiou, N. S., An Introduction to Nonlinear Analysis:. Applications. Kluwer Academic, Boston, 2003.Google Scholar
[6] Gasinski, L. and Papageorgiou, N. S., Nonsmooth Critical Point Theory and Nonlinear Boundary Value Problems. Series in Mathematical Analysis and Applications 8. Chapman and Hall/CRC Press, Boca Raton, FL, 2005.Google Scholar
[7] Granas, A., Guenther, R., Lee, J., and O’Regan, D., Boundary value problems on infinite intervals and semiconductor devices. J. Math. Anal. Appl. 116(1986), no. 2, 335–348.Google Scholar
[8] Hartman, P., Ordinary Differential Equations. Wiley, New York, 1964.Google Scholar
[9] Hu, S. and Papageorgiou, N. S., Handbook of Multivalued Analysis. I: Theory. Mathematics and Its Applications 419, Kluwer, Dordrecht, 1997.Google Scholar
[10] Ma, R., Existence of positive solutions for second-order boundary value problems on infinite intervals. Appl. Math. Letters, 16(2003), no. 1, 33–39.Google Scholar
[11] Nagumo, M., Über das Randwertproblem der nicht linearen gewöhnlichen Differentialgleichungen zweiter Ordnung. Proc. Phys.-Math. Soc. Japan 24(1942), 845–851.Google Scholar
[12] O’Regan, D., A note on Leray-Schauder alternatives for the decomposable maps of Bader. Nonlinear Anal., to appear.Google Scholar
[13] Wintner, A., The nonlocal existence problem of ordinary differential equations. Amer. J. Math. 67(1945), 277–284.Google Scholar